
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.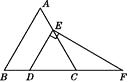
(1)求∠F的度数;
(2)若CD=2,求DF的长.
【答案】
(1)解:∵△ABC是等边三角形,
∴∠B=60°.
∵DE∥AB,
∴∠EDC=∠B=60°.
∵EF⊥DE,
∴∠DEF=90°.
∴∠F=90°-∠EDC=30° 。
(2)解:∵∠ACB=60°,∠EDC=60°,
∴∠DEC=60°.
∴△EDC是等边三角形.
∴DE=DC=2.
∵∠DEF=90°,∠F=30°,
∴DF=2DE=4 。
【解析】(1)根据等边三角形的性质得出∠B=60°,根据二直线平行同位角相等得出∠EDC=∠B=60°,根据垂直的定义得出∠DEF=90°,从而根据直角三角形的两锐角互余得出∠F=90°-∠EDC=30° ;
(2)根据三角形的内角和得出∠DEC=60°,根据三内角相等的三角形是等边三角形得出△EDC是等边三角形,根据等边三角形三边相等得出DE=DC=2,根据含30°的直角三角形的边之间的关系得出DF=2DE=4 。


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】下列等式从左到右的变形是因式分解的是( )
A.6a3b=3a2﹣2ab
B.(x+2)(x﹣2)=x2﹣4
C.2x2+4x﹣3=2x(x+2)﹣3
D.ax﹣ay=a(x﹣y)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AM⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
【特例探究】
(1)如图1,当tan∠PAB=1,c=4![]() 时,a= ,b= ;
时,a= ,b= ;
如图2,当∠PAB=30°,c=2时,a= ,b= ;
【归纳证明】
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
【拓展证明】
(3)如图4,ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3![]() ,AB=3,求AF的长.
,AB=3,求AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列因式分解正确的是( )
A. x2+9=(x+3)2 B. a2+2a+4=(a+2)2
C. a3-4a2=a2(a-4) D. 1-4x2=(1+4x)(1-4x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明用尺规作图作△ABC边AC上的高BH,作法如下:
①分别以点D,E为圆心,大于 ![]() DE的长为半径作弧,两弧交于F;
DE的长为半径作弧,两弧交于F;
②作射线BF,交边AC于点H;
③以B为圆心,BK长为半径作弧,交直线AC于点D和E;
④取一点K,使K和B在AC的两侧;
所以,BH就是所求作的高.其中顺序正确的作图步骤是( )
A.①②③④
B.④③②①
C.②④③①
D.④③①②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com