
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() ,垂足为点
,垂足为点![]() ,
,![]() ,垂足为点
,垂足为点![]() .则以下结论:①
.则以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,⑤
,⑤![]() ,其中正确的结论有( )
,其中正确的结论有( )
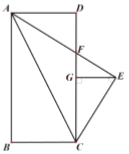
A.1个B.2个C.3个D.4个
【答案】D
【解析】
过点F作FH⊥AC,由角平分线的性质得到HF=DF,延长CE与AD的延长线交于点M,
又AF平分∠CAD,AF⊥CE,由“三线合一”逆定理,得到AC=AM,CE=EM.再设HF=DF=x,由等积法得到![]() ,从而求出关键的DF的值.利用勾股定理得到AC=AH=
,从而求出关键的DF的值.利用勾股定理得到AC=AH=![]() , 有DM=
, 有DM=![]() ,
,![]() ,所以CE=
,所以CE=![]() ,而后找到图中常见的相识三角形并利用其性质逐一推理计算判断即可.
,而后找到图中常见的相识三角形并利用其性质逐一推理计算判断即可.
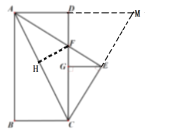
解:∵∠CEF=∠CEA=90°,∠CAE=∠EAD=∠FCE,
∴![]() ;
;
故① 对;
若![]() 成立,则易知∠BAC=∠EAC=∠FAD=30°,则在
成立,则易知∠BAC=∠EAC=∠FAD=30°,则在![]() 中BC=
中BC=![]() AB,而BC=2,AB=4,BC=
AB,而BC=2,AB=4,BC=![]() AB,故假设不成立. ②不对;
AB,故假设不成立. ②不对;
过点F作FH⊥AC,∵AF平分∠CAD,AD⊥DF,∴HF=DF=x,则CF=4-x,
又∵![]() ,
,
∵![]() ,
,
∴![]()
解得![]()
∴![]() ,
, ![]() ∴
∴![]() ,故④对;
,故④对;
又∵![]() ,
,
延长CE与AD的延长线交于点M,
∵AF平分∠CAD,AF⊥CE,
∴AC=AM=![]() ,CE=EM=
,CE=EM=![]() ,
,
∴DM=![]() ,又∵
,又∵![]()
∴![]()
∴![]() ,故③对;
,故③对;
∵∠CGE=∠ADF=90°,∠ECG=∠DAF,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴CG=DG=2,
又∵∠FEC=90°,GE⊥CF,
∴![]() ∽
∽![]() ,
,
∴![]() ,
,
∴ ![]() ,又∵CG=DG,
,又∵CG=DG,
∴![]() ∴⑤对;
∴⑤对;
综上有4个正确,
故选:D.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图1是长方体模型,棱长如图所示,图2是它的一种表面展开图.
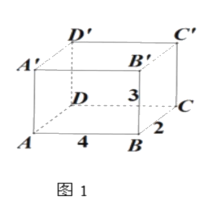
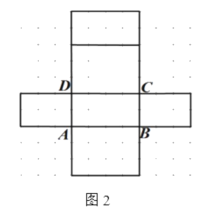

(1)①在图2中,表示出C可能的位置;
②在图3中画出长方体的一种展开图(不同于图2);
(2)图1中,一只在顶点A的蚂蚁,要吃到C处的甜食,求它沿长方体表面爬行的最短距离;
(3) 在满足AB+BC+BB=9的条件下,当AB为何值时,蚂蚁从A沿长方体表面爬行到C距离最短,并写出其中的一种方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
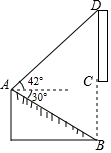
【题目】小婷在放学路上,看到隧道上方有一块宣传“中国﹣南亚博览会”的竖直标语牌CD.她在A点测得标语牌顶端D处的仰角为42°,测得隧道底端B处的俯角为30°(B,C,D在同一条直线上),AB=10m,隧道高6.5m(即BC=65m),求标语牌CD的长(结果保留小数点后一位).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
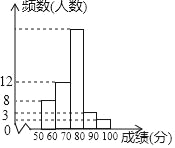
【题目】(7分)某中学1000名学生参加了”环保知识竞赛“,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)作为样本进行统计,并制作了如图频数分布表和频数分布直方图(不完整且局部污损,其中“■”表示被污损的数据).请解答下列问题:
成绩分组 | 频数 | 频率 |
50≤x<60 | 8 | 0.16 |
60≤x<70 | 12 | a |
70≤x<80 | ■ | 0.5 |
80≤x<90 | 3 | 0.06 |
90≤x≤100 | b | c |
合计 | ■ | 1 |
(1)写出a,b,c的值;
(2)请估计这1000名学生中有多少人的竞赛成绩不低于70分;
(3)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取两名同学参加环保知识宣传活动,求所抽取的2名同学来自同一组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.

(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三第一轮复习重在查漏补缺,课后很重要的一项任务是“纠错”.在深大附中九年级随机抽取部分学生进行调查,对平时的错题:![]() 表示“每一道错题都解决了”,
表示“每一道错题都解决了”,![]() 表示“大部分错题解决了”,
表示“大部分错题解决了”,![]() 表示“只有一部分错题解决了”,
表示“只有一部分错题解决了”,![]() 表示“从不解决错题”.对抽取的学生问卷统计后如图:
表示“从不解决错题”.对抽取的学生问卷统计后如图:
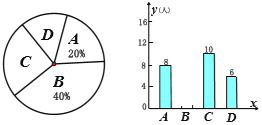
(1)抽查的学生有______人;扇形统计图中,![]() 占比_______;
占比_______;![]() 占比_______.
占比_______.
(2)补全条形统计图;
(3)全年级有480人,估计对错题“全解决”和“大部分解决”共有多少学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
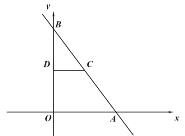
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,直线
为坐标原点,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,
,![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 匀速运动,同时点
匀速运动,同时点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 匀速运动,设点
匀速运动,设点![]() 运动的时间为
运动的时间为![]() 秒
秒![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)在(2)的条件下,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,点
,点![]() 为
为![]() 中点,连接
中点,连接![]() ,求
,求![]() 为何值时,直线
为何值时,直线![]() 与
与![]() 轴相交所成的锐角与
轴相交所成的锐角与![]() 互余.
互余.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (m,n 为常数).
(m,n 为常数).
(1)若抛物线的的对称轴为直线 x=1,且经过点(0,-1),求 m,n 的值;
(2)若抛物线上始终存在不重合的两点关于原点对称,求 n 的取值范围;
(3)在(1)的条件下,存在正实数 a,b( a<b),当 a≤x≤b 时,恰好有![]() ,请直接写出 a,b 的值.
,请直接写出 a,b 的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com