
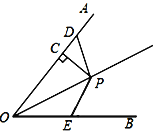
【题目】如图,P为∠AOB的平分线上一点,PC⊥OA于点C,D为OA上一点,E为OB上一点,∠ODP=180°-∠OEP.
(1)求证:PD=PE.
(2)若OC=6,求OD+OE的值.
【答案】(1)证明见解析;(2)12.
【解析】
(1)证明:作PH⊥OB于H点,根据角平分线的性质可得PH=PC,利用角角边定理可证△PDC≌△PEH,继而可得PD=PE;
(2)根据AAS就可以得出△CDP≌△EHP,从而得到CD=EH,进而得出DO+EO=12cm.
证明:作PH⊥OB于H点,
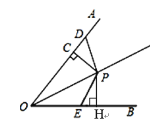
因为P为∠AOB的平分线上一点,PC⊥OA于点C,PH⊥OB于H点,
所以PH=PC,
因为∠ODP=180°-∠OEP,∠ PEH=180°-∠OEP,
所以∠ODP=∠ PEH,
所以∠PDC=∠ PEH,
在![]() 和
和![]() 中,
中,
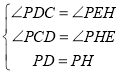
所以△PDC≌△PEH
所以PD=PE;
(2)由△PDC≌△PEH得,CD=EH,
∵DO+EO=DC+CO+EO,
∴DO+EO=EH+EO+CO,
∴DO+EO=HO+CO,
∴DO+EO=2CO,
∵CO=6cm,
∴DO+EO=12cm.


科目:初中数学 来源: 题型:
【题目】A,B两地相距60 km,甲、乙两人从两地出发相向而行,甲先出发.图中l1,l2表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:
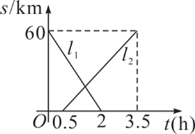
(1)表示乙离A地的距离与时间关系的图象是_____(填l1或l2);甲的速度是_____,乙的速度是_____
(2)甲出发多少小时两人恰好相距5 km?
查看答案和解析>>
科目:初中数学 来源: 题型:
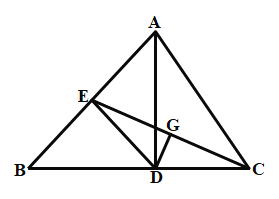
【题目】如图,在△ABC中,AD是高,CE是中线,DG垂直平分CE,连接DE.
(1)求证:DC=BE;
(2)若∠AEC=72°,求∠BCE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B,C分别在线段NM,NA上,在△ABC中,∠A∶∠ABC∶∠BCA=3∶5∶10,且△ABC≌△MNC,则∠BCM∶∠NBA等于( )

A.1∶2B.1∶3C.1∶4D.1∶5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为12 cm的正三角形,动点P从A向B以2 cm/s匀速运动,同时动点Q从B向C以1 cm/s匀速运动,当点P到达点B时,P,Q两点停止运动,设点P的运动时间为t秒,则当△PBQ为直角三角形时,t的值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
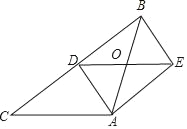
【题目】如图,在△ABC中,AB=AC,AD是BC边的中线,过点A作BC的平行线,过点B作AD的平行线,两线交于点E.
(1)求证:四边形ADBE是矩形;
(2)连结DE,交AB与点O,若BC=8,AO=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一个角是其邻角一半的圆内接四边形叫做圆内倍角四边形.
(1)如图1,四边形ABCD内接于⊙O,∠DCB﹣∠ADC=∠A,求证:四边形ABCD为圆内接倍角四边形;
(2)在(1)的条件下,⊙O半径为5.
①若AD为直径,且sinA=![]() ,求BC的长;
,求BC的长;
②若四边形ABCD中有一个角为60°,且BC=CD,则四边形ABCD的面积是 ;
(3)在(1)的条件下,记AB=a,BC=b,CD=c,AD=d,求证:d2﹣b2=ab+cd.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEB中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是

A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位运动员在距篮下4m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离是2.5m时,达到最大高度3.5m,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05m.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式.
(2)该运动员身高1.8m,在这次跳投中,球在头顶上0.25m处出手,
问:球出手时,他距离地面的高度是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com