
ЁОЬтФПЁПЧњОИЪаФГТЅХЬзМБИвдУПЦНЗНУз4000дЊЕФОљМлЖдЭтЯњЪлЃЌгЩгкЙњЮёдКгаЙиЗПЕиВњЕФаТеўВпГіЬЈКѓЃЌЙКЗПепГжБвЙлЭћЃЌЮЊСЫМгПьзЪН№жмзЊЃЌЗПЕиВњПЊЗЂЩЬЖдМлИёОЙ§СНДЮЯТЕїКѓЃЌОіЖЈвдУПЦНЗНУз3240дЊЕФОљМлПЊХЬЯњЪлЃЎ
ЃЈ1ЃЉЧѓЦНОљУПДЮЯТЕїЕФАйЗжТЪЃЛ
ЃЈ2ЃЉФГШЫзМБИвдПЊХЬМлОљМлЙКТђвЛЬз100ЦНЗНУзЕФзЁЗПЃЌПЊЗЂЩЬИјгшвдЯТСНжжгХЛнЗНАИвдЙЉбЁдёЃКЂйДђ9.9елЯњЪлЃЛЂкВЛДђелЃЌЫЭСНФъЮявЕЙмРэЗбЃЌЮявЕЙмРэЗбЪЧУПЦНЗНУзУПдТ1.4дЊЃЌЧыЮЪФФжжЗНАИИќгХЛнЃП
ЁОД№АИЁПЃЈ1ЃЉЦНОљУПДЮЯТЕїЕФАйЗжТЪЪЧ10%ЃЛ
ЃЈ2ЃЉбЁдёЗНАИЂкИќгХЛнЃЌРэгЩМћНтЮі.
ЁОНтЮіЁПЪдЬтЗжЮіЃК
ЃЈ1ЃЉЩшЦНОљУПДЮЯТЕїЕФАйЗжТЪЮЊ![]() ЃЌИљОнЬтвтСаГівЛдЊЖўДЮЗНГЬЃЌНтЗНГЬМДПЩЕУЕНЗћКЯвЊЧѓЕФД№АИЃЛ
ЃЌИљОнЬтвтСаГівЛдЊЖўДЮЗНГЬЃЌНтЗНГЬМДПЩЕУЕНЗћКЯвЊЧѓЕФД№АИЃЛ
ЃЈ2ЃЉИљОнЬтвтЗжБ№МЦЫуГіСНжжЗНАИЕФгХЛнН№ЖюЃЌдкБШНЯДѓаЁМДПЩЕУЕНД№АИЃЛ
ЪдЬтНтЮіЃК
ЃЈ1ЃЉЩшЦНОљУПДЮЯТЕїЕФАйЗжТЪЪЧxЃЌвРЬтвтЕУЃК
4000ЃЈ1ЉxЃЉ2=3240 ЃЌНтЕУЃКx=0.1=10%Лђx=1.9ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉ
ЁрЦНОљУПДЮЯТЕїЕФАйЗжТЪЪЧ10%
ЃЈ2ЃЉЗНАИЂйгХЛнН№Жю=100ЁС3240ЁСЃЈ1Љ99%ЃЉ=3240дЊЃЛ
ЗНАИЂкгХЛнН№Жю=100ЁС1.4ЁС12ЁС2=3360дЊЃЛ
Ёп3360>3240ЃЌ
ЙЪбЁдёЗНАИЂкИќгХЛн.


 ЬсЗжАйЗжАйМьВтОэЯЕСаД№АИ
ЬсЗжАйЗжАйМьВтОэЯЕСаД№АИ БІБДМЦЛЎЦкФЉГхДЬЖс100ЗжЯЕСаД№АИ
БІБДМЦЛЎЦкФЉГхДЬЖс100ЗжЯЕСаД№АИ ФмПМЪдШЋФм100ЗжЯЕСаД№АИ
ФмПМЪдШЋФм100ЗжЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИБжБНЧШ§НЧГпЕўЗХШчЭМ 1 ЫљЪОЃЌЯжНЋ 45ЁуЕФШ§НЧГпADE ЙЬЖЈВЛЖЏЃЌНЋКЌ 30ЁуЕФШ§НЧГп ABC ШЦЖЅЕу A ЫГЪБеызЊЖЏЃЈа§зЊНЧВЛГЌЙ§ 180 ЖШЃЉЃЌЪЙСНПщШ§НЧГпжСЩйгавЛзщБпЛЅЯрЦНааЃЎШчЭМ 2ЃКЕБЁЯBAD=15ЁуЪБЃЌBCЁЮDEЃЎдђЁЯBADЃЈ0ЁуЃМЁЯBADЃМ180ЁуЃЉЦфЫќЫљгаПЩФмЗћКЯЬѕМўЕФЖШЪ§ЮЊ________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋЫОЯњЪлвЛжжНјМлЮЊ![]() дЊ/ИіЕФМЦЫуЦїЃЌЦфЯњЪлСП
дЊ/ИіЕФМЦЫуЦїЃЌЦфЯњЪлСП![]() ЃЈЭђИіЃЉгыЯњЪлМлИё
ЃЈЭђИіЃЉгыЯњЪлМлИё![]() ЃЈдЊ/ИіЃЉЕФБфЛЏШчЯТБэЃК
ЃЈдЊ/ИіЃЉЕФБфЛЏШчЯТБэЃК
МлИё |
|
|
|
|
|
|
ЯњЪлСП |
|
|
|
|
|
|
ЭЌЪБЃЌЯњЪлЙ§ГЬжаЕФЦфЫћПЊжЇЃЈВЛКЌдьМлЃЉзмМЦ![]() ЭђдЊЃЎ
ЭђдЊЃЎ
ЃЈ![]() ЃЉЙлВьВЂЗжЮіБэжаЕФ
ЃЉЙлВьВЂЗжЮіБэжаЕФ![]() гы
гы![]() жЎМфЕФЖдгІЙиЯЕЃЌгУЫљбЇЙ§ЕФвЛДЮКЏЪ§ЃЌЗДБШР§КЏЪ§ЛђЖўДЮКЏЪ§ЕФгаЙижЊЪЖаДГі
жЎМфЕФЖдгІЙиЯЕЃЌгУЫљбЇЙ§ЕФвЛДЮКЏЪ§ЃЌЗДБШР§КЏЪ§ЛђЖўДЮКЏЪ§ЕФгаЙижЊЪЖаДГі![]() ЃЈЭђИіЃЉгы
ЃЈЭђИіЃЉгы![]() ЃЈдЊ/ИіЃЉЕФКЏЪ§НтЮіЪНЃЎ
ЃЈдЊ/ИіЃЉЕФКЏЪ§НтЮіЪНЃЎ
ЃЈ![]() ЃЉЧѓГіИУЙЋЫОЯњЪлетжжМЦЫуЦїЕФОЛЕУРћШѓ
ЃЉЧѓГіИУЙЋЫОЯњЪлетжжМЦЫуЦїЕФОЛЕУРћШѓ![]() ЃЈЭђИіЃЉгыЯњЪлМлИё
ЃЈЭђИіЃЉгыЯњЪлМлИё![]() ЃЈдЊ/ИіЃЉЕФКЏЪ§НтЮіЪНЃЌЯњЪлМлИёЖЈЮЊЖрЩйдЊЪБОЛЕУРћШѓзюДѓЃЌзюДѓжЕЪЧЖрЩйЃП
ЃЈдЊ/ИіЃЉЕФКЏЪ§НтЮіЪНЃЌЯњЪлМлИёЖЈЮЊЖрЩйдЊЪБОЛЕУРћШѓзюДѓЃЌзюДѓжЕЪЧЖрЩйЃП
ЃЈ![]() ЃЉИУЙЋЫОвЊЧѓОЛЕУРћШѓВЛФмЕЭгк
ЃЉИУЙЋЫОвЊЧѓОЛЕУРћШѓВЛФмЕЭгк![]() ЭђдЊЃЌЧыаДГіЯњЪлМлИё
ЭђдЊЃЌЧыаДГіЯњЪлМлИё![]() ЃЈдЊ/ИіЃЉЕФШЁжЕЗЖЮЇЃЎ
ЃЈдЊ/ИіЃЉЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
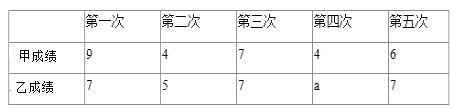
ЁОЬтФПЁПФГЙЋЫОЮЊНБРјдкШЄЮЖдЫЖЏЛсЩЯШЁЕУКУГЩМЈЕФдБЙЄЃЌМЦЛЎЙКТђМзЁЂввСНжжНБЦЗЙВ20МўЃЌЦфжаМзжжНБЦЗУПМў40дЊЃЌввжжНБЦЗУПМў30дЊЃЎ
ЃЈ1ЃЉШчЙћЙКТђМзЁЂввСНжжНБЦЗЙВЛЈЗбСЫ650дЊЃЌЧѓМзЁЂввСНжжНБЦЗИїЙКТђСЫЖрЩйМўЃЛ
ЃЈ2ЃЉШчЙћЙКТђввжжНБЦЗЕФМўЪ§ВЛГЌЙ§МзжжНБЦЗМўЪ§ЕФ2БЖЃЌзмЛЈЗбВЛГЌЙ§680дЊЃЌЧѓИУЙЋЫОгаФФМИжжВЛЭЌЕФЙКТђЗНАИЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩчЧјзМБИдкМзЁЂввСНЮЛЩфМ§АЎКУепжабЁГівЛШЫВЮМгМЏбЕЃЌСНШЫИїЩфСЫ5НЃЃЌЫћУЧЕФзмГЩМЈ![]() ЕЅЮЛЃКЛЗ
ЕЅЮЛЃКЛЗ![]() ЯрЭЌЃЌаЁгюИљОнЫћУЧЕФГЩМЈЛцжЦСЫЩаВЛЭъећЕФЭГМЦЭМБэЃЌВЂМЦЫуСЫМзГЩМЈЕФЦНОљЪ§КЭЗНВю
ЯрЭЌЃЌаЁгюИљОнЫћУЧЕФГЩМЈЛцжЦСЫЩаВЛЭъећЕФЭГМЦЭМБэЃЌВЂМЦЫуСЫМзГЩМЈЕФЦНОљЪ§КЭЗНВю![]() МћаЁгюЕФзївЕ
МћаЁгюЕФзївЕ![]() ЃЎ
ЃЎ

![]() ______ЃЌ
______ЃЌ![]() ______ЃЛ
______ЃЛ
![]() ЧыЭъГЩЭМжаввГЩМЈБфЛЏЧщПіЕФелЯпЃЛ
ЧыЭъГЩЭМжаввГЩМЈБфЛЏЧщПіЕФелЯпЃЛ
![]() ЙлВьФуВЙШЋЕФелЯпЭМПЩвдПДГі______
ЙлВьФуВЙШЋЕФелЯпЭМПЩвдПДГі______![]() ЬюЁАМзЁБЛђЁАввЁБ
ЬюЁАМзЁБЛђЁАввЁБ![]() ЕФГЩМЈБШНЯЮШЖЈ
ЕФГЩМЈБШНЯЮШЖЈ![]() ВЮееаЁгюЕФМЦЫуЗНЗЈЃЌМЦЫуввГЩМЈЕФЗНВюЃЌВЂбщжЄФуЕФХаЖЯЃЛВЂХаЖЯЫНЋБЛбЁжаЃЎ
ВЮееаЁгюЕФМЦЫуЗНЗЈЃЌМЦЫуввГЩМЈЕФЗНВюЃЌВЂбщжЄФуЕФХаЖЯЃЛВЂХаЖЯЫНЋБЛбЁжаЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФЗНГЬk2x2Љ2ЃЈk+1ЃЉx+1=0гаСНИіЪЕЪ§ИљЃЎ
ЃЈ1ЃЉЧѓkЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЕБk=1ЪБЃЌЩшЫљИјЗНГЬЕФСНИіИљЗжБ№ЮЊx1КЭx2ЃЌЧѓЃЈx1Љ2ЃЉЃЈx2Љ2ЃЉЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌADЮЊЕШБпЁїABCЕФИпЃЌEЁЂFЗжБ№ЮЊЯпЖЮADЁЂACЩЯЕФЖЏЕуЃЌЧвAEЃНCFЃЌЕБBFЃЋCEШЁЕУзюаЁжЕЪБЃЌЁЯAFBЃН_______ЁуЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁППьЕнЙЋЫОЮЊЬсИпПьЕнЗжМ№ЕФЫйЖШЃЌОіЖЈЙКТђЛњЦїШЫРДДњЬцШЫЙЄЗжМ№ЃЎвбжЊЙКТђМзаЭЛњЦїШЫ1ЬЈЃЌвваЭЛњЦїШЫ2ЬЈЃЌЙВаш14ЭђдЊЃЛЙКТђМзаЭЛњЦїШЫ2ЬЈЃЌвваЭЛњЦїШЫ3ЬЈЃЌЙВаш24ЭђдЊЃЎ
ЃЈ1ЃЉЧѓМзЁЂввСНжжаЭКХЕФЛњЦїШЫУПЬЈЕФМлИёИїЪЧЖрЩйЭђдЊЃЛ
ЃЈ2ЃЉвбжЊМзаЭКЭвваЭЛњЦїШЫУПЬЈУПаЁЪБЗжМ№ПьЕнЗжБ№ЪЧ1200МўКЭ1000МўЃЌИУЙЋЫОМЦЛЎзюЖргУ41ЭђдЊЙКТђ8ЬЈетСНжжаЭКХЕФЛњЦїШЫЃЌдђИУЙЋЫОИУШчКЮЙКТђЃЌВХФмЪЙЕУУПаЁЪБЕФЗжМ№СПзюДѓЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌAHЁЭBCЃЌBFЦНЗжЁЯABCЃЌBEЁЭBFЃЌEFЁЮBCЃЌвдЯТЫФИіНсТлЂйAHЁЭEFЃЌЂкЁЯABF=ЁЯEFBЃЌЂлACЁЮBEЃЌЂмЁЯE=ЁЯABE.е§ШЗЕФЪЧЃЈ ЁЁ ЃЉ

A. ЂйЂкЂлЂм B. ЂйЂк C. ЂйЂлЂм D. ЂйЂкЂм
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com