
【题目】某公司销售一种进价为![]() 元/个的计算器,其销售量
元/个的计算器,其销售量![]() (万个)与销售价格
(万个)与销售价格![]() (元/个)的变化如下表:
(元/个)的变化如下表:
价格 |
|
|
|
|
|
|
销售量 |
|
|
|
|
|
|
同时,销售过程中的其他开支(不含造价)总计![]() 万元.
万元.
(![]() )观察并分析表中的
)观察并分析表中的![]() 与
与![]() 之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出
之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出![]() (万个)与
(万个)与![]() (元/个)的函数解析式.
(元/个)的函数解析式.
(![]() )求出该公司销售这种计算器的净得利润
)求出该公司销售这种计算器的净得利润![]() (万个)与销售价格
(万个)与销售价格![]() (元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
(元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
(![]() )该公司要求净得利润不能低于
)该公司要求净得利润不能低于![]() 万元,请写出销售价格
万元,请写出销售价格![]() (元/个)的取值范围.
(元/个)的取值范围.
【答案】(1)![]() ;(2)将销售价格定为50元/个时,利润最大为50万元;(3)
;(2)将销售价格定为50元/个时,利润最大为50万元;(3)![]() .
.
【解析】试题分析:
(1)观察、分析表格中的数据可知,当售价每增加10元时,销售量都是减少1万个,因此![]() 与
与![]() 之间的函数关系是一次函数,由此可设
之间的函数关系是一次函数,由此可设![]() ,代入表格中的两组对应数据解出k、b即可得所求函数解析式;
,代入表格中的两组对应数据解出k、b即可得所求函数解析式;
(2)由净利润=销售收入-进货成本-其它开支,结合(1)中所得结果和已知即可列出函数关系式;把所得函数关系式配方化为“顶点式”即可得到所求的定价和最大利润;
(3)由(2)中所得解析式结合![]() 可解得对应的
可解得对应的![]() 的值,再结合(2)中所得函数的图象开口向下,即可得到对应的
的值,再结合(2)中所得函数的图象开口向下,即可得到对应的![]() 的取值范围.
的取值范围.
试题解析:
解:(![]() )根据表格数据:
)根据表格数据: ![]() 与
与![]() 为一次函数,设解析式
为一次函数,设解析式![]() ,
,
![]() ,解得
,解得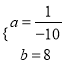 ,
,
∴解析式: ![]() .
.
(![]() )由题意得
)由题意得![]() ,
,
化简得![]() ,
,
故将销售价格定为![]() 元/个时,利润最大为
元/个时,利润最大为![]() 万元.
万元.
(![]() )当利润为
)当利润为![]() 万元时,
万元时, ![]() ,解得
,解得![]() ,
, ![]() ,
,
∵函数![]() 的图象开口向下,
的图象开口向下,
∴当利润不低于40万元时,销售价格的取值范围为![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )

A. 8![]() B. 8 C. 4
B. 8 C. 4![]() D. 6
D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“星光隧道”是贯穿新牌坊商圈和照母山以北的高端居住区的重要纽带,预计2017年底竣工通车,图中线段AB表示该工程的部分隧道,无人勘测飞机从隧道一侧的点A出发,沿着坡度为1:2的路线AE飞行,飞行至分界点C的正上方点D时,测得隧道另一侧点B的俯角为12°,继续飞行到点E,测得点B的俯角为45°,此时点E离地面高度EF=700米,则隧道BC段的长度约为( )米.(参考数据:tan12°≈0.2,cos12°≈0.98)
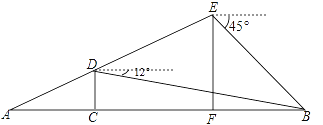
A. 2100 B. 1600 C. 1500 D. 1540
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王剪了两张直角三角形纸片,进行了如下的操作:

操作一:如图1,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
(1)如果AC=6cm,BC=8cm,可求得△ACD的周长为 ;
(2)如果∠CAD:∠BAD=4:7,可求得∠B的度数为 ;
操作二:如图2,小王拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,若AC=9cm,BC=12cm,请求出CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1+∠2=180°,∠B=∠3.

(1)判断DE与BC的位置关系,并说明理由:
解:结论:______________.
理由:∵∠1+∠2=180°,
∴_________________
∴∠ADE=∠3,
∵∠B=∠3
∴______________
∴DE∥BC;
(2)若∠C=65°,求∠DEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .在同一平面直线坐标系中
.在同一平面直线坐标系中
(![]() )若函数
)若函数![]() 的图象过点
的图象过点![]() ,函数
,函数![]() 的图象过点
的图象过点![]() ,求
,求![]() ,
, ![]() 的值.
的值.
(![]() )若函数
)若函数![]() 的图象经过
的图象经过![]() 的顶点.
的顶点.
①求证: ![]() .
.
②当![]() 时,比较
时,比较![]() ,
, ![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果手头没有硬币,下列方法可以模拟掷硬币实验的是( )

A. 掷一个瓶盖,盖面朝上代表正面,盖面朝下代表反面
B. 掷一枚图钉,钉尖着地代表正面,钉帽着地代表反面
C. 用计算器产生1和2两个随机整数,1代表正面,2代表反面
D. 转动如图所示的装盘,指针指向“红”代表正面,指针指向“蓝”代表反面
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】曲靖市某楼盘准备以每平方米4000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米3240元的均价开盘销售.
(1)求平均每次下调的百分率;
(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.9折销售;②不打折,送两年物业管理费,物业管理费是每平方米每月1.4元,请问哪种方案更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课外活动小组为了了解本校学生上网目的,随机调查了本校的部分学生,根据调查结果,统计整理并制作了如下尚不完整的统计图,根据以上信息解答下列问题:
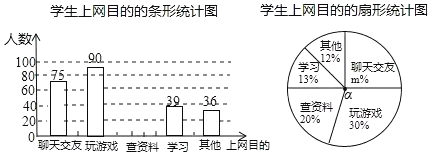
(1)参与本次调查的学生共有_____人;
(2)在扇形统计图中,m的值为_____;圆心角α=_____度.
(3)补全条形统计图;
(4)中学生上网玩游戏、聊天交友已经对正常的学习产生较多负面影响,为此学校计划开展一次“合理上网”专题讲座,每班随机抽取15名学生参加,小明所在的班级有50名学生,他被抽到听讲座的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com