练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，E，F分别是矩形ABCD的边AD，AB上的点，若EF=EC，且EF⊥EC．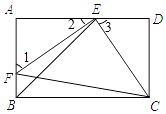
    （1）求证：△AEF≌△DCE；
    （2）若CD=1，求BE的长．

    【答案】
    （1）证明：在矩形ABCD中，∠A=∠D=90°，

    ∴∠1+∠2=90°，

    ∵EF⊥EC，

    ∴∠FEC=90°，

    ∴∠2+∠3=90°，

    ∴∠1=∠3，

    在△AEF和△DCE中，

    ，

    ∴△AEF≌△DCE（AAS）


    （2）解：由（1）知△AEF≌△DCE，

    ∴AE=DC=1，

    在矩形ABCD中，AB=CD=1，

    在R△ABE中，AB2+AE2=BE2，即12+12=BE2，

    ∴BE=


    【解析】（1）根据矩形的性质和已知条件可证明△AEF≌△DCE；（2）由（1）可知AE=DC，在Rt△ABE中由勾股定理可求得BE的长．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料：

    点A、B在数轴上分别表示两个数a、b，A、B两点间的距离记为|AB|，O表示原点．当A、B两点中有一点在原点时，不妨设点A为原点，如图1，则|AB|=|OB|=|b|=|a-b|；当A、B两点都不在原点时，

    ①如图2，若点A、B都在原点的右边时，|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|；

    ②如图3，若点A、B都在原点的左边时，|AB|=|OB|-|OA|=|b|-|a|=-b-（-a）=|a-b|；

    ③如图4，若点A、B在原点的两边时，|AB|=|OB|+|OA|=|b|+|a|=-b+a=|a-b|．

    回答下列问题：

    （1）综上所述，数轴上A、B两点间的距离为|AB|=______．

    （2）若数轴上的点A表示的数为3，点B表示的数为-4，则A、B两点间的距离为______；

    （3）若数轴上的点A表示的数为x，点B表示的数为-2，则|AB|=______，若|AB|=3，则x的值为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个多边形的每一个内角都相等，并且每个外角都等于和它相邻的内角的一半．

    （1）求这个多边形是几边形；

    （2）求这个多边形的每一个内角的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠AOB=30°，∠AOB内有一定点P，且OP=12，在OA上有一点Q，OB上有一点R，若△PQR周长最小，则最小周长是_____

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在读书月活动中，某校号召全体师生积极捐书，为了解所捐书籍的种类，图书管理员对部分书籍进行了抽样调查，根据调查数据绘制了如下不完整的统计图表．请你根据统计图表所提供的信息回答下面问题： 某校师生捐书种类情况统计表

    种类

    频数

    百分比

    A．科普类

    12

    30%

    B．文学类

    n

    35%

    C．艺术类

    m

    20%

    D．其它类

    6

    15%


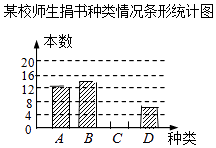
    （1）统计表中的n= ， 并补全条形统计图；
    （2）本次活动师生共捐书2000本，请估计有多少本科普类图书？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校计划在“阳光体育”活动课程中开设乒乓球、羽毛球、篮球、足球四个体育活动项目供学生选择．为了估计全校学生对这四个活动项目的选择情况，体育老师从全体学生中随机抽取了部分学生进行调查（规定每人必须并且只能选择其中的一个项目），并把调查结果绘制成如图所示的不完整的条形统计图和扇形统计图，请你根据图中信息解答下列问题：

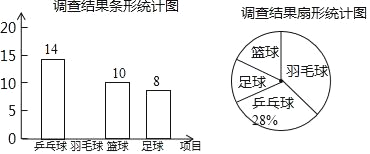
    （1）求参加这次调查的学生人数，并补全条形统计图；

    （2）求扇形统计图中“篮球”项目所对应扇形的圆心角度数；

    （3）若该校共有600名学生，试估计该校选择“足球”项目的学生有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，OM是∠AOC的平分线，ON是∠BOC的平分线．

    （1）如图1，当∠AOB是直角，∠BOC=60°时，∠MON的度数是多少？

    （2）如图2，当∠AOB=α，∠BOC=60°时，猜想∠MON与α的数量关系；

    （3）如图3，当∠AOB=α，∠BOC=β时，猜想∠MON与α、β有数量关系吗？如果有，指出结论并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=﹣ x2+bx+c与y轴交于点C，与x轴交于A、B两点（点A在原点左侧，点B在原点右侧），且∠ACB=90°，tan∠BAC= ． ①求抛物线的解析式；
    ②若抛物线顶点为P，求四边形APCB的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图1，线段AB、CD相交于点O，连接AD、CB，我们把形如图1的图形称之为“8字形”．试解答下列问题：

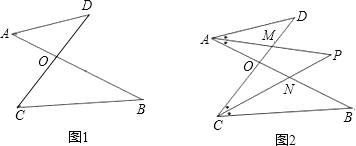
    （1）在图1中，请直接写出∠A、∠B、∠C、∠D之间的数量关系：　 　；

    （2）仔细观察，在图2中“8字形”的个数：　 　个；

    （3）在图2中，若∠D=40°，∠B=36°，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．利用（1）的结论，试求∠P的度数；

    （4）如果图2中∠D和∠B为任意角时，其他条件不变，试问∠P与∠D、∠B之间存在着怎样的数量关系．（直接写出结论即可）

    查看答案和解析>>

    同步练习册答案