
【题目】如图,抛物线y=﹣ ![]() x2+bx+c与y轴交于点C,与x轴交于A、B两点(点A在原点左侧,点B在原点右侧),且∠ACB=90°,tan∠BAC=
x2+bx+c与y轴交于点C,与x轴交于A、B两点(点A在原点左侧,点B在原点右侧),且∠ACB=90°,tan∠BAC= ![]() . ①求抛物线的解析式;
. ①求抛物线的解析式;
②若抛物线顶点为P,求四边形APCB的面积.
【答案】解:①令x=0则y=﹣ ![]() x2+bx+c=c, ∴C(0,c),
x2+bx+c=c, ∴C(0,c),
∵tan∠BAC= ![]() ,
,
∴A(﹣2c,0),
∠ACB=90°,
∴∠BCO=∠BAC,
∴OB= ![]() OC=
OC= ![]() c,
c,
∴B( ![]() c,0),
c,0),
把A(﹣2c,0),B( ![]() c,0)代入y=﹣
c,0)代入y=﹣ ![]() x2+bx+c=c得,
x2+bx+c=c得, 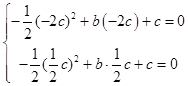 ,
,
解得:  ,
,
求抛物线的解析式为y=﹣ ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() ;
;
②y=﹣ ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() =﹣
=﹣ ![]() (x+
(x+ ![]() )2+
)2+ ![]() ,
,
∴P(﹣ ![]() ,
, ![]() ),
),
令﹣ ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() =0,解得:x1=﹣1,x2=
=0,解得:x1=﹣1,x2= ![]() ,
,
∴A(﹣1,0),B( ![]() ,0)
,0)
连接AP,PC,CB,PO,则四边形APCB的面积=S△AOP+S△POC+S△COB= ![]() ×1×
×1× ![]() +
+ ![]() ×
× ![]() ×
× ![]() +
+ ![]() ×
× ![]() ×
× ![]() =
= ![]()
【解析】①由y=﹣ ![]() x2+bx+c=c,可求得C(0,c),由tan∠BAC=
x2+bx+c=c,可求得C(0,c),由tan∠BAC= ![]() ,可设A(﹣2c,0),B(
,可设A(﹣2c,0),B( ![]() c,0),把A(﹣2c,0),B(
c,0),把A(﹣2c,0),B( ![]() c,0)代入y=﹣
c,0)代入y=﹣ ![]() x2+bx+c=c求得b,c,即可求得求抛物线的解析式; ②解方程﹣
x2+bx+c=c求得b,c,即可求得求抛物线的解析式; ②解方程﹣ ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() =0可求得A,B点的坐标,由于四边形APCB的面积=S△AOP+S△POC+S△COB , 根据三角形的面积公式即可求得结论.
=0可求得A,B点的坐标,由于四边形APCB的面积=S△AOP+S△POC+S△COB , 根据三角形的面积公式即可求得结论.
【考点精析】认真审题,首先需要了解抛物线与坐标轴的交点(一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.),还要掌握解直角三角形(解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法))的相关知识才是答题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知A(m,n),且满足m-2+(n-2)2=0,过A作AB⊥y轴,垂足为B.
(1)求A点坐标;
(2)如图1,分别以AB,AO为边作等边△ABC和△AOD,试判定线段AC和DC的数量关系和位置关系,并说明理由;
(3)如图2,过A作AE⊥x轴,垂足为E,点F、G分别为线段OE、AE上的两个动点 (不与端点重合),满足∠FBG=45°,设OF=a,AG=b,FG=c,试探究![]() 的值是 否为定值?如果是,直接写出此定值:如果不是,请举例说明.
的值是 否为定值?如果是,直接写出此定值:如果不是,请举例说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC. 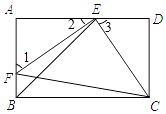
(1)求证:△AEF≌△DCE;
(2)若CD=1,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C
处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最
短距离为 ▲ cm.
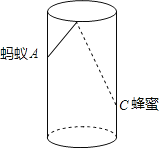
查看答案和解析>>
科目:初中数学 来源: 题型:
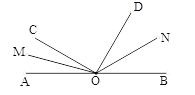
【题目】如图所示,∠AOB是平角,OM、ON分别是∠AOC、∠BOD 的平分线.
(1)知∠AOC=40°,∠BOD=60°,求∠MON的度数;
(2)知∠COD=90°,求出∠MON的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料:
一般地,n个相同的因数a相乘:![]() 记为
记为![]() .如23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).
.如23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).
一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).
问题:
(1)计算以下各对数的值:log24=______,log216=______,log264=______.
(2)观察(1)中三数4、16、64之间满足怎样的关系式为______log24、log216、log264之间又满足怎样的关系式:______
(3)由(2)的结果,你能归纳出一个一般性的结论吗?logaM+logaN=______(a>o且a≠1,M>0,N>0).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘渔船位于灯塔P的北偏东30°方向,距离灯塔18海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东55°方向上的B处,此时渔船与灯塔P的距离约为海里(结果取整数)(参考数据:sin55°≈0.8,cos55°≈0.6,tan55°≈1.4).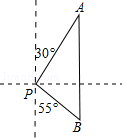
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,若△CEF的面积为12cm2,则S△DGF的值为( )
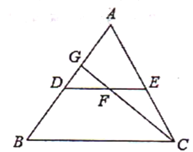
A.4cm2 B.6cm2 C.8cm2 D.9cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,则FM的长为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com