
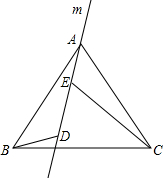
 如图,直线m经过正三角形ABC的顶点A,在直线m上取两点D,E,使得使∠ADB=∠AEC=120°.通过观察或测量,猜想线段BD,CE与DE之间满足的数量关系,并予以证明.
如图,直线m经过正三角形ABC的顶点A,在直线m上取两点D,E,使得使∠ADB=∠AEC=120°.通过观察或测量,猜想线段BD,CE与DE之间满足的数量关系,并予以证明.
|


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
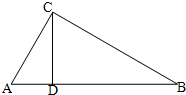 如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm.(1)求△ABC的面积;(2)求CD的长.
如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm.(1)求△ABC的面积;(2)求CD的长.查看答案和解析>>
科目:初中数学 来源: 题型:
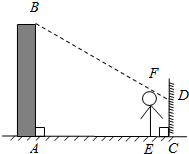 李航想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,李航边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得李航落在墙上的影子高度CD=1.2m,CE=0.6m,CA=30m(点A、E、C在同一直线上).已知李航的身高EF是1.6m,请你帮李航求出楼高AB.
李航想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,李航边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得李航落在墙上的影子高度CD=1.2m,CE=0.6m,CA=30m(点A、E、C在同一直线上).已知李航的身高EF是1.6m,请你帮李航求出楼高AB.查看答案和解析>>
科目:初中数学 来源: 题型:
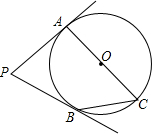 如图,PA、PB是⊙O的两条切线,A、B为切点,AC为⊙O的直径,∠P=70°,则∠PBC=( )
如图,PA、PB是⊙O的两条切线,A、B为切点,AC为⊙O的直径,∠P=70°,则∠PBC=( )| A、110° | B、120° |
| C、135° | D、145° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com