
����Ŀ��ij��Ʒ���ڵ��ۼ�Ϊÿ��28Ԫ��ÿ����۳�24�����г����鷢�֣��ۼ�ÿ����1Ԫ��ÿ���������2������֪����Ʒ�Ľ���Ϊÿ��20Ԫ�������Ʒÿ���������Ϊy�����ۼ�Ϊÿ��xԪ��xΪ��������
��1����y��x֮��ĺ�����ϵʽ��
��2������Ʒ���ۼ۶�Ϊÿ������Ԫʱ��ÿ�����������P��Ԫ�������������Ƕ���Ԫ��
��3�������۲��Ź涨����Ʒÿ�����ۼ۲��ø���32Ԫ����Ҫÿ���õ�������182Ԫ����ֱ��д������Ʒ���ۼ�x��Ԫ����ȡֵ��Χ���� ����
���𰸡�![]()
��������
��1�����������ڵ��ۼ�Ϊÿ��28Ԫ��ÿ����۳�24�����ۼ�ÿ����1Ԫ��ÿ���������2�������г�y��x�ĺ�����ϵʽ��
��2��������=�����������ۼ�-���ۣ��õ�������ϵʽ�������ö��κ�����������⣻
��3�����y=182ʱx��ֵ������������ö��κ��������ʿɵ�ÿ��������182Ԫʱx��ȡֵ��Χ��
�⣺��1��������ã�y=24-2��x-28��=-2x+80��
����y��x֮��ĺ�����ϵʽΪy=-2x+80��
��2��������ã�P=��x-20��y=��x-20����-2x+80��![]() ��
��
���Ե�x=30ʱ��Pȡ���ֵ200��
����Ʒ���ۼ۶�Ϊÿ��30Ԫʱ��ÿ�����������P��Ԫ��������������200Ԫ��
��3����y=182ʱ����![]() ��
��
��ã�![]() ��
��
��Ϊÿ�����ۼ۲��ø���32Ԫ��
��27��x��32ʱ��ÿ���õ�������182Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����IΪ��ABC�����ģ�AB=4��AC=3��BC=2������ACBƽ��ʹ�䶥����I�غϣ���ͼ����Ӱ���ֵ��ܳ�Ϊ��������
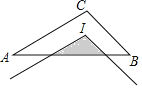
A. 4.5 B. 4 C. 3 D. 2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
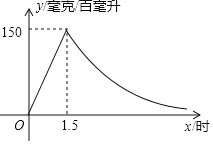
����Ŀ��ʵ��������ʾ��һ����˺Ȱ��ͶȰƺ�1.5Сʱ����ѪҺ�оƾ�����y������/�ٺ�������ʱ��x��ʱ������������1.5Сʱ����1.5Сʱ��y��x�ɷ�����������ͼ���ṩ����Ϣ������������⣺
��1��д��һ����˺Ȱ��ͶȰƺ�y��x֮��ĺ�����ϵʽ����Ӧ���Ա���ȡֵ��Χ��
��2�������ҹ涨��������ʻ��ԱѪҺ�еľƾ��������ڻ����20����/�ٺ���ʱ���ڡ��ƺ��ʻ�������ܼݳ���·������������ѧģ�ͣ�����ij��ʻԱ����21��00�ڼҺ�����ͶȰƣ��ڶ�������7��00�ܷ�ݳ�ȥ�ϰࣿ��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��C��D�ǰ�ԲO�ϵ����ȷֵ㣬ֱ��AB=4������AD��AC��DE��AB������ΪE��DE��AC�ڵ�F��
��1�����AFE�Ķ�����
��3������Ӱ���ֵ��������������к��ţ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y��ax2��bx��c��a��0���Ĵ���ͼ����ͼ��ʾ��1��x��h��2��0��xA��1�������н��ۣ��� 2a��b��0���� abc��0���� ��OC��2OA����2b��ac = 4���� 3a��c��0��������ȷ�ĸ����ǣ� ��
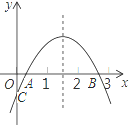
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ����һ�߳�Ϊl��������OABC����OA��OC�ֱ���x�ᡢy���ϣ�����ԶԽ���OBΪ�����ڶ���������OBB1C1�����ԶԽ���OBlΪ����������������OBlB2C2���մ˹�������ȥ�����B2020������Ϊ__________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳��ٰ�齱����������£��ڲ����Ĵ�������2�������2��������Щ�����ɫ�ⶼ��ͬ���˿�ÿ������һ������������������1�ݽ�Ʒ��������������û�н�Ʒ��
��1�����С��ֻ��һ��������ᣬ��ôС����ý�Ʒ�ĸ���Ϊ ����
��2�����С��������������ᣨ�����Żأ�����С�����2�ݽ�Ʒ�ĸ��ʡ�������������״ͼ�������б����ȷ���д���������̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�������������ֱ�ΪA��1��1����B��4��2����C��3��4����
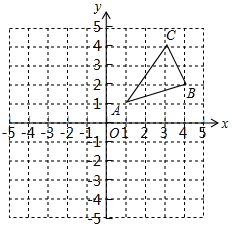
��1���뻭����ABC����ƽ��5����λ���Ⱥ�õ�����A1B1C1��
��2���뻭����ABC����ԭ��ԳƵ���A2B2C2��
��3����ֱ���ж��ı���CBC2B2����״��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCO�Ķ���A��C�ֱ���y�ᡢx���ϣ���ABΪ�ҵġ�M��x������.����A������Ϊ��0��8������Բ��M������Ϊ__________.
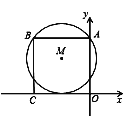
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com