
【题目】如图,边长为4的正方形ABCD内接于⊙O,点E是![]() 上的一个动点(不与A、B重合),点F是
上的一个动点(不与A、B重合),点F是![]() 上的一点,连接OE、OF,分别与AB、BC交于点G、H,且∠EOF=90°,有下列结论: ①
上的一点,连接OE、OF,分别与AB、BC交于点G、H,且∠EOF=90°,有下列结论: ①![]() ; ②△OGH是等腰直角三角形; ③四边形OGBH的面积不随点E位置的变化而变化; ④△GBH周长的最小值为
; ②△OGH是等腰直角三角形; ③四边形OGBH的面积不随点E位置的变化而变化; ④△GBH周长的最小值为![]() .其中错误的是______.(把你认为错误结论的序号填上)
.其中错误的是______.(把你认为错误结论的序号填上)
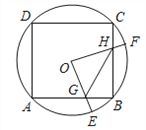
【答案】④
【解析】分析:连接OC、OB、BE,对于①,根据ASA可证△BOE≌△COF,根据全等三角形的性质得到BE=CF,根据等弦对等弧得到![]() ,可以判断①;
,可以判断①;
对于②,根据SAS可证△BOG≌△COH,根据全等三角形的性质得到∠GOH=90°,OG=OH,根据等腰直角三角形的判定得到△OGH是等腰直角三角形,可以判断②;
过O作OM⊥BC,ON⊥AB,对于③,通过证明△HOM≌△GON,可得四边形OGBH的面积始终等于正方形ONBM的面积,可以判断③;
对于④,根据△BOG≌△COH可知BG=CH,则BG+BH=BC=4,设BG=x,则BH=4-x,根据勾股定理得到GH,可以求得其最小值,可以判断④.
详解:①如图所示,连接OC、OB、BE.
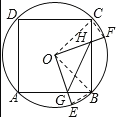
∵∠BOE+∠BOF=90°,∠COF+∠BOF=90°,
∴∠BOE=∠COF,
∵在△BOE与△COF中,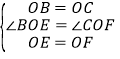 ,
,
∴△BOE≌△COF,
∴BE=CF,
∴![]() ,①正确;
,①正确;
②∵BE=CF,
∴△BOG≌△COH.
∵∠BOG=∠COH,∠COH+∠OBF=90°,
∴∠GOH=90°,OG=OH,
∴△OGH是等腰直角三角形,②正确.
③如图所示,过O作OM⊥BC,ON⊥AB.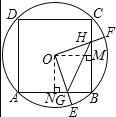
∵△HOM≌△GON,
∴四边形OGBH的面积始终等于正方形ONBM的面积,③正确;
④∵△BOG≌△COH,
∴BG=CH,
∴BG+BH=BC=4,
设BG=x,则BH=4-x,
则GH=![]() ,∴其最小值为4+2
,∴其最小值为4+2![]() ,④错误.
,④错误.
故答案为④.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2k+1)x+k2=0①有两个不相等的实数根.
(1)求k的取值范围;
(2)设方程①的两个实数根分别为x1,x2,当k=1时,求x12+x22的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46;B:46.5~53.5;C:53.5﹣60.5:D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.解答下列问题.
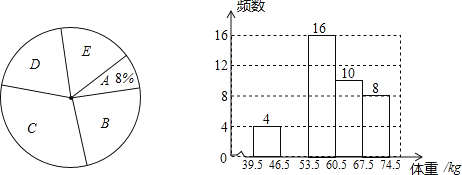
(1)这次一共抽取了 名学生,并补全频数直方图;
(2)C组学生的人数所占的百分比为 ;
(3)在扇形统计图中D组的圆心角是 度;
(4)请你估计该校初三年级体重超过60kg的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知△ABC,AB=AC,以边AB为直径的⊙O交BC于点D,交AC于点E,连接DE.
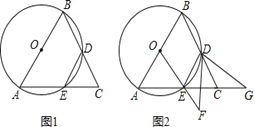
(1)求证:DE=DC.
(2)如图2,连接OE,将∠EDC绕点D逆时针旋转,使∠EDC的两边分别交OE的延长线于点F,AC的延长线于点G.试探究线段DF、DG的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点C,D在线段AB上(点C,D不与线段AB的端点重合),AC+DB=![]() AB.
AB.
(1)若AB=6,请画出示意图并求线段CD的长;
(2)试问线段CD上是否存在点E,使得CE=![]() AB,请说明理由.
AB,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区计划对面积为1200m2的区域进行绿化.经投标,由甲、乙两个工程队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天.
(1)甲、乙两施工队每天分别能完成绿化的面积是多少?
(2)设先由甲队施工x天,再由乙队施工y天,刚好完成绿化任务,求y与x的函数解析式;
(3)在(2)的情况下,若甲队绿化费用为1600元/天,乙队绿化费用为700元/天,在施工过程中每天需要支付高温补贴a元(100≤a≤300),且工期不得超过14天,则如何安排甲,乙两队施工的天数,使施工费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三江夜游项目是宁波市月光经济和“三江六岸”景观提升的重要工程,一艘游轮从周宿夜江游船码头到宁波大剧院游船码头顺流而行用40分钟,从宁波大剧院游船码头沿原线返回周宿夜江游船码头用了1小时,已知游轮在静水中的平均速度为8千米/小时,求水流的速度.设水流的速度为x千米/小时,则可列方程为( )
A.40(8-x)=1×(8+x) B.![]() (8+x)=8 C.
(8+x)=8 C.![]() (8+x)=8-x D.
(8+x)=8-x D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com