
【题目】如图,△ABC中,AD平分∠BAC,
(1)图①中,已知AF⊥BC , ∠B=500,∠C=600. 求∠DAF的度数.

(2)图②中,请你在直线AD上任意取一点E(不与点A、D重合),画EF⊥BC,垂足为F.已知∠B=α,∠C=β(β>a).求∠DEF的度数. (用α、β的代数式表示)
【答案】(1)∠DAF=5°(2)∠DEF=![]() (β-α)
(β-α)
【解析】试题分析:根据三角形的内角和定理可求得∠BAC的度数,又因AD平分∠BAC,根据角平分线的定义可求得∠CAD的度数,再由垂直的定义可得∠AFC的度数,根据直角三角形的两锐角互余即可求得∠DAF的度数;(2)如图2,根据三角形的内角和定理可求得∠BAC的度数,又因AD平分∠BAC,根据角平分线的定义可求得∠CAD的度数,再由三角形的内角和定理求得∠ADC的度数,再由垂直的定义可得∠EFD的度数,根据直角三角形的两锐角互余即可求得∠DEF的度数;如图3,类比图2的方法解决问题即可.
试题解析:
(1)∵∠B=500,∠C=600,
∴∠BAC=180°-∠B-∠C=180°-500-600 =70°,
∵AD平分∠BAC,
∴∠CAD = ![]() ∠BAC =
∠BAC =![]() ×70°=35°,
×70°=35°,
又∵AF⊥BC ,
∴∠AFC =90°,
∴∠CAF =90° -∠C =30°,
∴ ∠DAF =∠CAD -∠CAF =5°.
(2)① 如图,
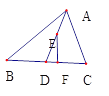
图2
∵∠B=α,∠C=β,
∴∠BAC=180°-∠B-∠C=180°-(α+β),
∵AD平分∠BAC,
∴∠CAD = ![]() ∠BAC =
∠BAC =![]() [180°-(α+β)]=90°-
[180°-(α+β)]=90°-![]() (α+β),
(α+β),
∴∠ADC=180°-∠CAD-∠C=180°-[90°-![]() (α+β)]- β=90°+
(α+β)]- β=90°+![]() α-
α-![]() β
β
又∵EF⊥BC ,
∴∠EFD=90°,
∴∠DEF =90° -∠ADC =90°-[90°+![]() α-
α-![]() β]=
β]= ![]() (β-α).
(β-α).
②如图,
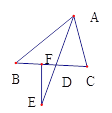
图3
∵∠B=α,∠C=β,
∴∠BAC=180°-∠B-∠C=180°-(α+β),
∵AD平分∠BAC,
∴∠CAD = ![]() ∠BAC =
∠BAC =![]() [180°-(α+β)]=90°-
[180°-(α+β)]=90°-![]() (α+β),
(α+β),
∴∠ADC=180°-∠CAD-∠C=180°-[90°-![]() (α+β)]- β=90°+
(α+β)]- β=90°+![]() α-
α-![]() β
β
∴∠ADC=∠EDF=90°+![]() α-
α-![]() β,
β,
又∵EF⊥BC ,
∴∠EFD=90°,
∴∠DEF =90° -∠EDF =90°-[90°+![]() α-
α-![]() β]=
β]= ![]() (β-α).
(β-α).


科目:初中数学 来源: 题型:
【题目】已知:点A在射线CE上,∠C=∠D.
(1)如图1,若AC∥BD,求证:AD∥BC;
(2)如图2,若∠BAC=∠BAD,BD⊥BC,请探究∠DAE与∠C的数量关系,写出你的探究结论,并加以证明;
(3)如图3,在(2)的条件下,过点D作DF∥BC交射线于点F,当∠DFE=8∠DAE时,求∠BAD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天,一蔬菜经营户用60元钱从蔬菜批发市场批了西红柿和豆角共40㎏到菜市场去卖,西红柿和豆角这天的批发价与零售价如下表所示:问:他当天卖完这些西红柿和豆角能赚多少钱?
品名 | 西红柿 | 豆角 |
批发价(单位:元/kg) | 1.2 | 1.6 |
零售价(单位:元/kg) | 1.8 | 2.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
(1)求证:△ABE≌△ACD;
(2)求证:DC⊥BE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:AB∥CD,直线l交AB、CD分别于点E、F,点M在EF上,N是直线CD上的一个动点(点N不与F重合)
(1)当点N在射线FC上运动时,∠FMN+∠FNM=∠AEF,说明理由;
(2)当点N在射线FD上运动时,∠FMN+∠FNM与∠AEF有什么关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
(1)画出△ABC的AB边上的中线CD;
(2)画出△ABC向右平移4个单位后得到的△A1B1C1;
(3)图中AC与A1C1的关系是: ;
(4)图中,能使S△ABQ=S△ABC的格点Q(点Q不与点C重合),共有 个.

查看答案和解析>>
科目:初中数学 来源: 题型:
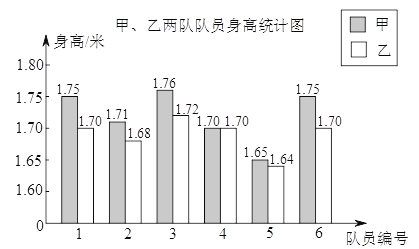
【题目】某学校要成立一支由6名女生组成的礼仪队,八年级两个班各选6名女生,分别组成甲队和乙队参加选拔.每位女生的身高统计如图,部分统计量如下表:
平均数 | 标准差 | 中位数 | |
甲队 | 1.72 | 0.038 | |
乙队 | 0.025 | 1.70 |
(1)求甲队身高的中位数;
(2)求乙队身高的平均数及身高不小于1.70米的频率;
(3)如果选拔的标准是身高越整齐越好,那么甲、乙两队
中哪一队将被录取?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( ).
A. “打开电视机,正在播放《动物世界》”是必然事件
B. 某种彩票的中奖概率为![]() ,说明每买1000张,一定有一张中奖
,说明每买1000张,一定有一张中奖
C. 抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为![]()
D. 想了解长沙市所有城镇居民的人均年收入水平,宜采用抽样调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在四边形ABCD中, ![]() ,延长BC至点E,连接AE交CD于点F,使
,延长BC至点E,连接AE交CD于点F,使![]()
![]() 求证:
求证: ![]() ;
;
![]() 求证:
求证: ![]() ;
;
![]() 若BF平分
若BF平分![]() ,请写出
,请写出![]() 与
与![]() 的数量关系______
的数量关系______![]() 不需证明
不需证明![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com