
【题目】已知二次函数![]() 的图象如图所示,解决下列问题:
的图象如图所示,解决下列问题:

![]() 关于
关于![]() 的一元二次方程
的一元二次方程![]() 的解为________;
的解为________;
![]() 求此抛物线的解析式;
求此抛物线的解析式;
![]() 当
当![]() 为值时,
为值时,![]() ;
;
![]() 若直线
若直线![]() 与抛物线没有交点,直接写出
与抛物线没有交点,直接写出![]() 的范围.
的范围.
【答案】(1) -1或3 ;(2) y=-x+2x+3; (3) x>3或x<-1;(4)k>4.
【解析】
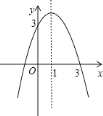
(1)直接观察图象,抛物线与x轴交于-1,3两点,所以方程的解为![]() .
.
(2)设出抛物线的顶点坐标形式,代入坐标(3,0),即可求得抛物线的解析式.
(3)若y<0,则函数的图象在x轴的下方,找到对应的自变量取值范围即可.
(4)若直线y=k与抛物线没有交点,则k>函数的最大值即可.
(1)观察图象可看对称轴出抛物线与x轴交于x=-1和x=3两点,
∴方程的解为![]() ,
,
故答案为:-1或3;
![]() 设抛物线解析式为
设抛物线解析式为![]() ,
,
∵抛物线与![]() 轴交于点
轴交于点![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴抛物线解析式为![]() ,
,
即:抛物线解析式为![]() ;
;
![]() 若
若![]() ,则函数的图象在
,则函数的图象在![]() 轴的下方,由函数的图象可知:
轴的下方,由函数的图象可知:![]() 或
或![]() ;
;
![]() 若直线
若直线![]() 与抛物线没有交点,则
与抛物线没有交点,则![]() 函数的最大值4,即
函数的最大值4,即![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,弦BC,DE相交于点F,且DE⊥AB于点G,过点C作⊙O的切线交DE的延长线于点H.
(1)求证:HC=HF;
(2)若⊙O的半径为5,点F是BC的中点,tan∠HCF=m,写出求线段BC长的思路.

查看答案和解析>>
科目:初中数学 来源: 题型:
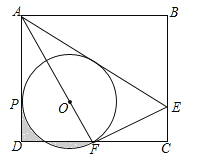
【题目】(2017四川省达州市,第16题,3分)如图,矩形ABCD中,E是BC上一点,连接AE,将矩形沿AE翻折,使点B落在CD边F处,连接AF,在AF上取点O,以O为圆心,OF长为半径作⊙O与AD相切于点P.若AB=6,BC=![]() ,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=
,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=![]() CE;④
CE;④![]() .其中正确结论的序号是__________.
.其中正确结论的序号是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰![]() 中,
中,![]() ,
,![]() ,
,![]() 于点
于点![]() ,点
,点![]() 是
是![]() 延长线上一点,点
延长线上一点,点![]() 是线段
是线段![]() 上一点,
上一点,![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() 是等边三角形;④
是等边三角形;④![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )

A.1B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:通过小学的学习我们知道,分数可分为“真分数”和“假分数”,而假分数都可化为带分数,如:![]() 我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.
我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.
如![]() 这样的分式就是假分式;再如:
这样的分式就是假分式;再如:![]() ,
,![]() 这样的分式就是真分式
这样的分式就是真分式![]() 类似的,假分式也可以化为带分式(即:整式与真分式的和的形式)
类似的,假分式也可以化为带分式(即:整式与真分式的和的形式)
如:![]() ;
;
解决下列问题:
(1)分式![]() 是______分式(填“真分式”或“假分式”);
是______分式(填“真分式”或“假分式”);
(2)将假分式![]() 化为带分式;
化为带分式;
(3)如果x为整数,分式![]() 的值为整数,求所有符合条件的x的值.
的值为整数,求所有符合条件的x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2k-1)x+k2=0有两个实根x1和x2
(1) 求实数k的取值范围
(2) 若方程两实根x1、x2满足x12-x22=0,求k的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(0,4),B(8,0),C(8,4),连接AC,BC得到四边形AOBC,点D在边AC上,连接OD,将边OA沿OD折叠,点A的对应点为点P,若点P到四边形AOBC较长两边的距离之比为1:3,则点P的坐标为__________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,CD与⊙O相切于C,BE∥CO.
(1)求证:BC是∠ABE的平分线;
(2)若DC=8,⊙O的半径OA=6,求CE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com