
分析 (1)首先根据点A(5,0)到x轴的距离是0,到y轴的距离是5,可得d(∠xOy,A)=0+5=5;然后根据点B(3,2)到x轴的距离是2,到y轴的距离是3,求出d(∠xOy,B)的值是多少即可.
(2)首先设点P的坐标是(x,y),然后根据d(∠xOy,P)=5,可得x+y=5,据此求出点P运动所形成的图形即可.
(3)①首先作CE⊥OT于点E,CF⊥x轴于点F,延长FC交OT于点H,则CF=1,然后设直线OT对应的函数关系式为y=$\frac{4}{3}$x(x≥0),求出点H的坐标为H(4,$\frac{16}{3}$),进而求出CH,OH的值各是多少;最后根据相似三角形判定的方法,判断出△HEC∽△HFO,即可判断出$\frac{EC}{FO}$=$\frac{HC}{HO}$,据此求出EC的值,即可求出d(∠xOT,C)的值是多少.
②首先作QG⊥OT于点G,QH⊥x轴于点H,交OT于点K,设点Q的坐标为(m,n),其中3≤m≤5,则n=-$\frac{1}{2}$m2+2m+$\frac{5}{2}$,然后判断出点K的坐标,以及HK,OK的大小,再判断出Rt△QGK∽Rt△OHK,即可判断出$\frac{QG}{OH}=\frac{QK}{OK}$,据此求出QG=$\frac{4m-3n}{5}$;最后求出d(∠xOT,Q)的值,根据二次函数最值的求法,求出当d(∠xOT,Q)取最大值时点Q 的坐标即可.
解答 解:(1)∵点A(5,0)到x轴的距离是0,到y轴的距离是5,
∴d(∠xOy,A)=0+5=5,
∵点B(3,2)到x轴的距离是2,到y轴的距离是3,
∴d(∠xOy,B)=2+3=5.
综上,可得d(∠xOy,A)=5,d(∠xOy,B)=5.
(2)设点P的坐标是(x,y),
∵d(∠xOy,P)=5,
∴x+y=5,
∴点P运动所形成的图形是线段y=5-x(0≤x≤5).
(3)①如图3,作CE⊥OT于点E,CF⊥x轴于点F,延长FC交OT于点H,则CF=1,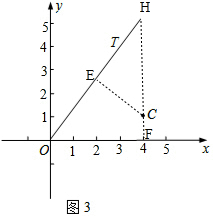 ,
,
∵直线OT对应的函数关系式为y=$\frac{4}{3}$x(x≥0),
∴点H的坐标为H(4,$\frac{16}{3}$),
∴CH=$\frac{16}{3}-1$=$\frac{13}{3}$,OH=$\sqrt{{OF}^{2}{+FH}^{2}}$=$\sqrt{{4}^{2}{+(\frac{16}{3})}^{2}}$=$\frac{20}{3}$,
∵CE⊥OT,
∴∠OHF+∠HCE=90°,
又∵∠OHF+∠HOF=90°,
∴∠HCE=∠HOF,
在△HEC和△HFO中,
$\left\{\begin{array}{l}{∠HCE=∠HOF}\\{∠HEC=∠HFO}\end{array}\right.$
∴△HEC∽△HFO,
∴$\frac{EC}{FO}$=$\frac{HC}{HO}$,
即 $\frac{EC}{4}$=$\frac{\frac{13}{3}}{\frac{20}{3}}=\frac{13}{20}$,
∴EC=$\frac{13}{5}$,
∴d(∠xOT,C)=$\frac{13}{5}$+1=$\frac{18}{5}$.
②如图4,作QG⊥OT于点G,QH⊥x轴于点H,交OT于点K,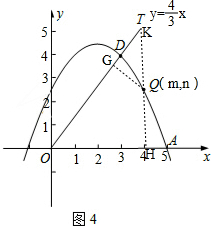 ,
,
设点Q的坐标为(m,n),其中3≤m≤5,
则n=-$\frac{1}{2}$m2+2m+$\frac{5}{2}$,
∴点K的坐标为(m,$\frac{4}{3}$m),QK=$\frac{4}{3}m-n$,
∴HK=$\frac{4}{3}$m,OK=$\frac{5}{3}$m.
∵Rt△QGK∽Rt△OHK,
∴$\frac{QG}{OH}=\frac{QK}{OK}$,
∴QG=$\frac{4m-3n}{5}$,
∴d(∠xOT,Q)=QG+QH
=$\frac{4m-3n}{5}$+n
=$\frac{4}{5}m+\frac{2}{5}n$
=$\frac{4}{5}m+\frac{2}{5}$(-$\frac{1}{2}$m2+2m+$\frac{5}{2}$)
=-$\frac{1}{5}$m2+$\frac{8}{5}$m+1
=$-\frac{1}{5}$(m-4)2$+\frac{21}{5}$
∵3≤m≤5,
∴当m=4时,d(∠AOB,Q)取得最大值$\frac{21}{5}$.
此时,点Q的坐标为(4,$\frac{5}{2}$).
故答案为:5、5.
点评 (1)此题主要考查了二次函数综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合思想的应用,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力.
(2)此题还考查了相似三角形判定的方法和性质的应用,以及二次函数最值的求法,要熟练掌握.
(3)此题还考查了“点角距”的含义和求法,要熟练掌握.


科目:初中数学 来源:2017届湖北省赤壁市九年级下学期第一次模拟(调研)考试数学试卷(解析版) 题型:解答题
如图,在□ABCD中,F是AD的中点,延长BC到点E,使CE=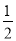 BC,连结DE,CF。
BC,连结DE,CF。
(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
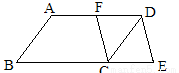
 如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别为A(-2,3)、B(-3,1).
如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别为A(-2,3)、B(-3,1).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在直角坐标系中,过点P(x,0)作x轴的垂线分别交抛物线y=x2+2与直线y=-$\frac{1}{2}$x于A,B两点,以线段AB为对角线作正方形ADBC,已知点Q(a,b)为该抛物线上的点.
如图,在直角坐标系中,过点P(x,0)作x轴的垂线分别交抛物线y=x2+2与直线y=-$\frac{1}{2}$x于A,B两点,以线段AB为对角线作正方形ADBC,已知点Q(a,b)为该抛物线上的点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
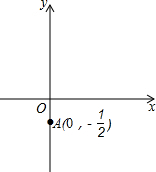 已知:在平面直角坐标系xoy中,抛物线y=ax2+bx+c与直线y=mx+n相交于
已知:在平面直角坐标系xoy中,抛物线y=ax2+bx+c与直线y=mx+n相交于查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线L是第一、三象限的角平分线.
如图,在平面直角坐标系中,直线L是第一、三象限的角平分线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com