
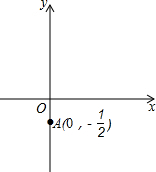 ��֪����ƽ��ֱ������ϵxoy�У�������y=ax2+bx+c��ֱ��y=mx+n�ཻ��
��֪����ƽ��ֱ������ϵxoy�У�������y=ax2+bx+c��ֱ��y=mx+n�ཻ������ ��1���ٰ�A������ֱ���������ߺ�ֱ�߽���ʽ���ɷֱ����c��n��ֵ���ڰ�B��������������߽���ʽ����Ϣ����������a��ֵ��
��2���������ɵó������߽���ʽ��ֱ�߽���ʽ����P��PQ��y�ᣬ��ֱ��AB�ڵ�Q����P������Ϊ��x��axx
x2+bx+c������ɱ�ʾ��Q�����꣬�Ӷ��ɱ�ʾ��PQ�ij����ɱ�ʾ����PAB������������ö��κ��������ʿ���������ֵ������á�ABP�����ȡֵ��Χ��
��3��������õ������߽���ʽ����ö������ꡢx=1��x=-1ʱ��Ӧ��yֵ���ٷ�-$\frac{b}{2}$��-1��-1��-$\frac{b}{2}$��0��0��-$\frac{b}{2}$��1��-$\frac{b}{2}$��1��������ֱ�����y�����ֵ���������������y=ax2+bx+c�ϵ�x��������ĵ�����꣮
��� �⣺
��1���١�n������y=ax2+bx+c��ֱ��y=mx+n�ཻ��A��0��-$\frac{1}{2}$����
���A��������������߽���ʽ�ɵ�c=-$\frac{1}{2}$������ֱ�߽���ʽ�ɵ�n=-$\frac{1}{2}$��
�ʴ�Ϊ��-$\frac{1}{2}$��-$\frac{1}{2}$��
�ڡ�B��m-b��m2-mb+n����������y=ax2+bx+c�ϣ�
��m2-mb+n=a��m-b��2+b��m-b��+c��
��c=n=-$\frac{1}{2}$��
��m2-mb=a��m-b��2+b��m-b���������ɵã�a-1����m-b��=0��
��A��B���غϣ�
��m-b��0��
��a-1=0�����a=1��
�ʴ�Ϊ��1��
��2����m=1��b=-2����ֱ��AB����ʽΪy=x-$\frac{1}{2}$�������߽���ʽΪy=x2-2x-$\frac{1}{2}$��
��ͼ����P��PQ��y�ᣬ��ֱ��AB�ڵ�Q��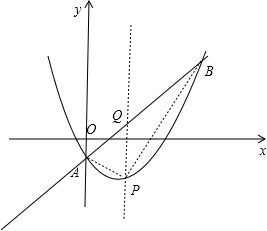
��P��x��x2-2x-$\frac{1}{2}$������Q��x��x-$\frac{1}{2}$����
��P����ֱ��AB�·���
��PQ=��x-$\frac{1}{2}$��-��x2-2x-$\frac{1}{2}$��=-x2+3x��
��B��3��$\frac{5}{2}$����
���B��PQ�ľ���Ϊ3-x����A��PQ�ľ���Ϊx��
��S��PAB=$\frac{1}{2}$��-x2+3x����3-x��+$\frac{1}{2}$��-x2+3x��x=$\frac{1}{2}$��-x2+3x����3=-$\frac{3}{2}$��x2-3x��=-$\frac{3}{2}$��x-$\frac{3}{2}$��2+$\frac{27}{8}$
���ABP��������ֵΪ$\frac{27}{8}$��
���ABP�����ȡֵ��ΧΪ��0��S��$\frac{27}{8}$��
��3��������y=x2+bx-$\frac{1}{2}$�ĶԳ���Ϊx=-$\frac{b}{2}$����СֵΪ-$\frac{{b}^{2}+2}{4}$��
��x=-1ʱ��y=$\frac{1}{2}$-b����x=1ʱ��y=$\frac{1}{2}$+b��
�ٵ�x=-$\frac{b}{2}$��-1����b��2ʱ��
|$\frac{1}{2}$+b|-|$\frac{1}{2}$-b|=$\frac{1}{2}$+b+$\frac{1}{2}$-b=1��0��
��x��������ĵ������Ϊ��1��$\frac{1}{2}$+b����
�ڵ�-1��-$\frac{b}{2}$��0����0��b��2ʱ��
|$\frac{1}{2}$+b|-|-$\frac{{b}^{2}+2}{4}$|=$\frac{1}{2}$+b-$\frac{{b}^{2}+2}{4}$=b��1-$\frac{b}{4}$����0��
�ൽx��������ĵ������Ϊ��1��$\frac{1}{2}$+b����
�۵�0��-$\frac{b}{2}$��1����-2��b��0ʱ��
|$\frac{1}{2}$-b|-|-$\frac{{b}^{2}+2}{4}$|=$\frac{1}{2}$-b-$\frac{{b}^{2}+2}{4}$=-b��1+$\frac{b}{4}$����0��
�ൽx��������ĵ������Ϊ��-1��$\frac{1}{2}$-b����
�ܵ�x=-$\frac{b}{2}$��1����b��-2ʱ��
|$\frac{1}{2}$+b|-|$\frac{1}{2}$-b|=-$\frac{1}{2}$-b-��$\frac{1}{2}$-b��=-1��0��
�ൽx��������ĵ������Ϊ��-1��$\frac{1}{2}$-b����
������������b��0ʱ����x��������ĵ������Ϊ��1��$\frac{1}{2}$+b����
��b��0ʱ����x��������ĵ������Ϊ��-1��$\frac{1}{2}$-b����
���� ������Ҫ������κ������ۺ�Ӧ�ã��漰����ϵ�����������ε���������κ��������ʡ��������۵�֪ʶ���ڣ�1����ע�����ϵ�����IJ��裬�ڣ�2������P�������ʾ����PAB������ǽ���Ĺؼ����ڣ�3���а�����ת�������������ֵ�ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�������ϴ��ۺ��Ժ�ǿ���ѶȽϴ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016-2017ѧ������ʡ���������꼶��ѧ�ڵ�һ���¿���ѧ�Ծ��������棩 ���ͣ���ѡ��
���и�ʽ�У�����ƽ���ʽ������� �� ��
A. 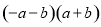 B.
B. 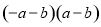
C. 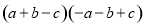 D.
D. 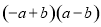
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
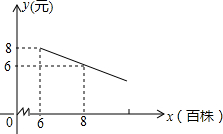 ij����ƻ���100����������һ�ֻ��ܣ����ڹ������ۣ���֪����������г���������ĵ���Ϊy��Ԫ��������x�����֮꣩��Ĺ�ϵ��ͼ��ʾ������x��6���������������飬ÿ��Ļ��ܹ���Ӧ����ÿ����������6�꣬ÿ������۵���Ϊ26Ԫ��ÿ������ÿ����1�꣬ÿ������۵��۾ͼ���2Ԫ��
ij����ƻ���100����������һ�ֻ��ܣ����ڹ������ۣ���֪����������г���������ĵ���Ϊy��Ԫ��������x�����֮꣩��Ĺ�ϵ��ͼ��ʾ������x��6���������������飬ÿ��Ļ��ܹ���Ӧ����ÿ����������6�꣬ÿ������۵���Ϊ26Ԫ��ÿ������ÿ����1�꣬ÿ������۵��۾ͼ���2Ԫ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
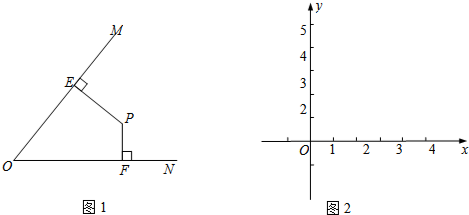
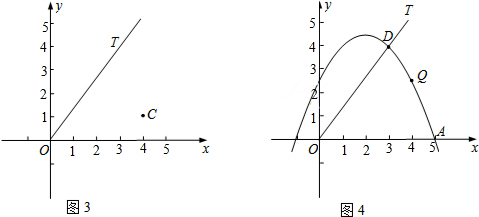
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
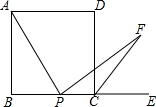 ��E��������ABCD�ı�BC�ӳ�����һ�㣬��P��BC������һ�㣬AP��PF����AP=PF������CF��
��E��������ABCD�ı�BC�ӳ�����һ�㣬��P��BC������һ�㣬AP��PF����AP=PF������CF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
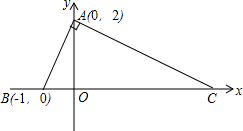 ��ͼ��ƽ��ֱ������ϵ�У�AB��AC��
��ͼ��ƽ��ֱ������ϵ�У�AB��AC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
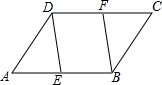 ��?ABCD�У���E��F�ֱ���AB��CD�ϣ���DEA=��BFC����֤���ı���DEBFΪƽ���ı��Σ�
��?ABCD�У���E��F�ֱ���AB��CD�ϣ���DEA=��BFC����֤���ı���DEBFΪƽ���ı��Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com