
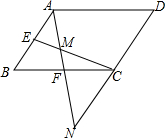
 如图,在?ABCD中,E、F分别为AB、BC的中点,连接EC、AF,AF与EC交于点M,AF的延长线与DC的延长线交于点N.
如图,在?ABCD中,E、F分别为AB、BC的中点,连接EC、AF,AF与EC交于点M,AF的延长线与DC的延长线交于点N.分析 (1)由在?ABCD中,E、F分别为AB、BC的中点,易证得△ABF≌△NCF(AAS),继而证得结论;
(2)由AB∥DN,易证得△AEM∽△NCM,然后由相似三角形的对应边成比例,且E、F分别为AB、BC的中点,求得$\frac{AM}{MN}=\frac{AE}{CN}=\frac{1}{2}$,然后由$BE=\frac{1}{2}AB$,AB=2n,BE=2MF,AF=FN,求得AN=3n.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥DN,
∴∠B=∠FCN,∠BAF=∠N,
∵F是BC的中点,
∴BF=CF,
在△ABF和△NCF中,
$\left\{\begin{array}{l}{∠B=∠FCN}\\{∠BAF=∠N}\\{BF=CF}\end{array}\right.$,
∴△ABF≌△NCF(AAS),
∴AB=CN;
(2)解:∵AB∥DN,
∴△AEM∽△NCM,
∴$\frac{AM}{MN}=\frac{AE}{CN}$,
∵AB=CN,且E是AB的中点,
∴$\frac{AM}{MN}=\frac{AE}{CN}=\frac{1}{2}$,
∵$BE=\frac{1}{2}AB$,AB=2n,BE=2MF,
∴BE=n,$MF=\frac{1}{2}n$,
∴$\frac{AF-MF}{FN+MF}=\frac{1}{2}$,
由△ABF≌△NCF,可得AF=FN,
∴$\frac{{AF-\frac{1}{2}n}}{{AF+\frac{1}{2}n}}=\frac{1}{2}$,
∴$AF=\frac{3}{2}n$,
∴AN=3n.
点评 此题考查了平行四边形的性质、相似三角形的判定与性质以及全等三角形的判定与性质.注意借助于全等三角形与相似三角形的性质求解是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
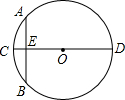 “圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言可表达为:“如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1寸,AB=10寸,则直径CD的长为多少?
“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言可表达为:“如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1寸,AB=10寸,则直径CD的长为多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
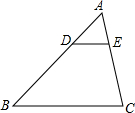 如图△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{4}$,求:
如图△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{4}$,求:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
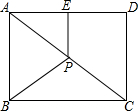 如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( )
如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为( )| A. | 14 | B. | 16 | C. | 17 | D. | 18 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
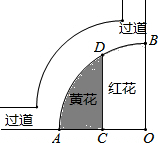 如图,某实践小组要在广场一角的扇形区域内种植红、黄两种花,半径OA=4米,C是OA的中点,点D在$\widehat{AB}$上,CD∥OB,则图中种植黄花(即阴影部分)的面积是$\frac{8}{3}$π-2$\sqrt{3}$(结果保留π).
如图,某实践小组要在广场一角的扇形区域内种植红、黄两种花,半径OA=4米,C是OA的中点,点D在$\widehat{AB}$上,CD∥OB,则图中种植黄花(即阴影部分)的面积是$\frac{8}{3}$π-2$\sqrt{3}$(结果保留π).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
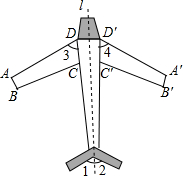 如图是轴对称图形.图中直线1是它的对称轴.
如图是轴对称图形.图中直线1是它的对称轴.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com