
【题目】如图,已知直线l1:y1=2x+1与坐标轴交于A、C两点,直线l2:y2=﹣x﹣2与坐标轴交于B、D两点,两直线的交点为P点.
(1)求P点的坐标;
(2)求△APB的面积;
(3)x轴上存在点T,使得S△ATP=S△APB,求出此时点T的坐标.
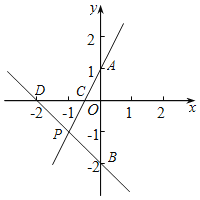
【答案】(1)P(﹣1,﹣1);(2)![]() ;(3)T(1,0)或(﹣2,0).
;(3)T(1,0)或(﹣2,0).
【解析】
(1)解析式联立构成方程组,该方程组的解就是交点坐标;
(2)利用三角形的面积公式解答;
(3)求得C的坐标,因为S△ATP=S△APB,S△ATP=S△ATC+S△PTC=|x+![]() |,所以|x+
|,所以|x+![]() |=
|=![]() ,解得即可.
,解得即可.
解:(1)由![]() ,解得
,解得![]() ,
,
所以P(﹣1,﹣1);
(2)令x=0,得y1=1,y2=﹣2
∴A(0,1),B(0,﹣2),
则 S△APB=![]() ×(1+2)×1=
×(1+2)×1=![]() ;
;
(3)在直线l1:y1=2x+1中,令y=0,解得x=﹣![]() ,
,
∴C(﹣![]() ,0),
,0),
设T(x,0),
∴CT=|x+![]() |,
|,
∵S△ATP=S△APB,S△ATP=S△ATC+S△PTC=![]() |x+
|x+![]() |(1+1)=|x+
|(1+1)=|x+![]() |,
|,
∴|x+![]() |=
|=![]() ,
,
解得x=1或﹣2,
∴T(1,0)或(﹣2,0).


科目:初中数学 来源: 题型:
【题目】证明题:本题须有完整过程,需要括号中的理由,只限本学期所学
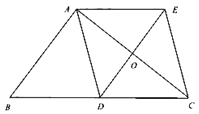
如图,在![]() 中,
中,![]() 是边
是边![]() 上的中线,
上的中线,![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,求证:四边形
,求证:四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A、B分别在x轴与y轴上,已知OA=6,OB=10.点D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒2个单位的速度沿线段AC﹣CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
(1)当点P经过点C时,求直线DP的函数解析式;
(2)①求△OPD的面积S关于t的函数解析式;
②如图②,把长方形沿着OP折叠,点B的对应点B′恰好落在AC边上,求点P的坐标.
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.



查看答案和解析>>
科目:初中数学 来源: 题型:
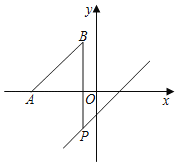
【题目】如图,在平面直角坐标系xOy中,点B(﹣1,3),点A(﹣5,0),点P是直线y=x﹣2上一点,且∠ABP=45°,则点P的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).

(1)当t为何值时,以A,P,M为顶点的三角形与△ABC相似?
(2)是否存在某一时刻t,使四边形APNC的面积S有最小值?若存在,求S的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,点 D 是边 BC 上的点(与 B、C 两点不重合),过点 D作 DE∥AC,DF∥AB,分别交 AB、AC 于 E、F 两点,下列说法正确的是( )

A. 若 AD 平分∠BAC,则四边形 AEDF 是菱形
B. 若 BD=CD,则四边形 AEDF 是菱形
C. 若 AD 垂直平分 BC,则四边形 AEDF 是矩形
D. 若 AD⊥BC,则四边形 AEDF 是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举行“中国梦我的梦”演讲比赛.小明和小红都想去,于是老师制作了三张形状、大小和颜色完全一样的卡片,上面分别标有“1”,“2”,“3”,小明从这三张卡片中随机抽取一张,记下数字后放回,小红再从这三张卡片中随机抽取一张并记下数字,谁抽取的数大就谁去,若两个数一样大则重新抽.这个游戏公平吗?请用树枝状图或列表的方法,结合概率知识给予说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图甲和图乙分别是A,B两家酒店去年下半年的月营业额(单位:百万元)统计图.
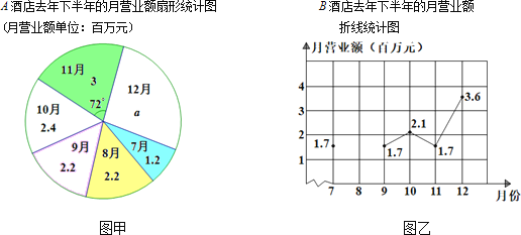
(1)求A酒店12月份的营业额a的值.
(2)已知B酒店去年下半年的月平均营业额为2.3百万元,求8月份的月营业额,并补全折线统计图.
(3)完成下面的表格(单位:百万元)
![]()
(4)综合以上分析,你认为哪一些数据更能较为准确的反映酒店的经营业绩?你认为哪家酒店的经营状况较好?请简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() (m是常数,m≠0),一次函数y=ax+b(a、b为常数,a≠0),其中一次函数与x轴,y轴的交点分别是A(-4,0),B(0,2).
(m是常数,m≠0),一次函数y=ax+b(a、b为常数,a≠0),其中一次函数与x轴,y轴的交点分别是A(-4,0),B(0,2).
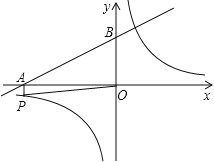
(1)求一次函数的关系式;
(2)反比例函数图象上有一点P满足:①PA⊥x轴;②PO=![]() (O为坐标原点),求反比例函数的关系式;
(O为坐标原点),求反比例函数的关系式;
(3)求点P关于原点的对称点Q的坐标,判断点Q是否在该反比例函数的图象上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com