
【题目】如图,平面直角坐标系中,菱形OABC的边OA在x轴正半轴上,OA=10,cos∠COA=![]() .一个动点P从点O出发,以每秒1个单位长度的速度沿线段OA方向运动,过点P作PQ⊥OA,交折线段OC﹣CB于点Q,以PQ为边向右作正方形PQMN,点N在射线OA上,当P点到达A点时,运动结束.设点P的运动时间为t秒(t>0).
.一个动点P从点O出发,以每秒1个单位长度的速度沿线段OA方向运动,过点P作PQ⊥OA,交折线段OC﹣CB于点Q,以PQ为边向右作正方形PQMN,点N在射线OA上,当P点到达A点时,运动结束.设点P的运动时间为t秒(t>0).
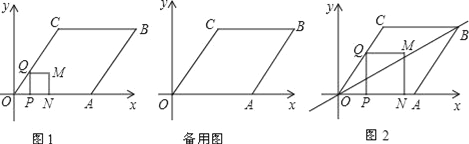
(1)C点的坐标为 ,当t= 时N点与A点重合;
(2)在整个运动过程中,设正方形PQMN与菱形OABC的重合部分面积为S,直接写出S与t之间的函数关系式和相应的自变量t的取值范围;
(3)如图2,在运动过程中,过点O和点B的直线将正方形PQMN分成了两部分,请问是否存在某一时刻,使得被分成的两部分中有一部分的面积是菱形面积的![]() ?若存在,请求出对应的t的值;若不存在,请说明理由.
?若存在,请求出对应的t的值;若不存在,请说明理由.
【答案】(1)t=![]() 时,N点与A点重合;(2)①
时,N点与A点重合;(2)①![]() ,
,
②![]() ,
,
③![]() ,
,
④8<t≤10,S=104﹣8t;
(3)①当0<t≤6,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
若![]() ,则
,则![]() ,
,![]() ,
,
若![]() ,则
,则![]() ,
,![]() ,
,
②当6<t≤8,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
若![]() ,则
,则![]() ,t=0(舍),
,t=0(舍),
若![]() ,则
,则![]() ,t3=8;
,t3=8;
③8<t≤10,不存在符合条件的t值.
【解析】试题分析:(1)根据菱形的性质得出OA=OC,再根据三角函数求出点C的坐标即可;
(2)根据面积公式列出函数关系式,注意动点运动时的几种情况,得出自变量的取值范围;
(3)根据被分成的两部分中有一部分的面积是菱形面积的![]() ,画出图示,分几种情况进行讨论解答.
,画出图示,分几种情况进行讨论解答.
试题解析:(1)∵菱形OABC中,OA=10,
∴OC=10,
∵cos∠COA=![]() ,
,
∴点C的坐标为:(6,8),
∵动点P从点O出发,以每秒1个单位长度的速度沿线段OA方向运动,
∵OA=10,
∴t=![]() 时,N点与A点重合;
时,N点与A点重合;
(2)①![]() ,
,
②![]() ,
,
③![]() ,
,
④8<t≤10,S=104﹣8t;
(3)S菱形=80,直线OB过原点(0,0),B点(16,8),故直线OB解析式为![]() ,
,
直线OB与PQ、MN分别交于E、F点,如图:
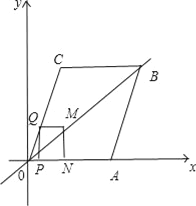
①当0<t≤6,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
若![]() ,则
,则![]() ,
,![]() ,
,
若![]() ,则
,则![]() ,
,![]() ,
,
②当6<t≤8,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
若![]() ,则
,则![]() ,t=0(舍),
,t=0(舍),
若![]() ,则
,则![]() ,t3=8;
,t3=8;
③8<t≤10,不存在符合条件的t值.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列说法:(1)无限小数是无理数;(2)无理数都是带根号的数;(3)任何实数都可以开立方;(4)有理数都是实数.其中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校全体同学喜欢的NBA篮球明星的情况,小明抽取了七年级一班50名同学进行调查,得到最喜欢的NBA篮球明星的调查结果如下:
A A B C D A B A A C B A A C B C A A B C A A B A C
D B A C D B A C D A A B C D A C B A C A C D C A A
其中:A代表姚明,B代表科比,C代表詹姆斯,D代表麦迪.
填表:
明星 | 划记 | 人数 |
A | ||
B | ||
C | ||
D |
(2)该班同学喜欢最多的是谁?
(3)你认为小明所选取的样本是随机调查的样本吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
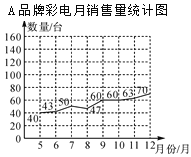
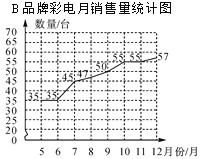
【题目】某家电商场A、B两种品牌彩电2016年5~12月销售量统计如图.
(1)有人认为B品牌彩电销售量比A品牌彩电销售量增长快.你同意这种观点吗?
(2)根据统计图进行比较、判断时要注意些什么?
(3)如果你是商场经理,从上面的统计图中你能得到哪些信息?对你有什么帮助?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
我们知道![]() 的几何意义是在数轴上数
的几何意义是在数轴上数![]() 对应的点与原点的距离;即
对应的点与原点的距离;即![]() ;这个结论可以推广为
;这个结论可以推广为![]() 表示在数轴上数
表示在数轴上数![]() ,
, ![]() 对应点之间的距离.绝对值的几何意义在解题中有着广泛的应用:
对应点之间的距离.绝对值的几何意义在解题中有着广泛的应用:
例1:解方程![]() .
.
容易得出,在数轴上与原点距离为4的点对应的数为±4,即该方程的![]() ±4;
±4;
例2:解方程![]() .
.
由绝对值的几何意义可知,该方程表示求在数轴上与-1和2的距离之和为5的点对应的![]() 的值.在数轴上,-1和2的距离为3,满足方程的
的值.在数轴上,-1和2的距离为3,满足方程的![]() 对应的点在2的右边或在-1的左边.若
对应的点在2的右边或在-1的左边.若![]() 对应的
对应的
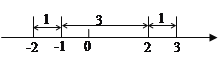
点在2的右边,如图可以看出![]() ;同理,若
;同理,若![]() 对应点在-1的左边,可得
对应点在-1的左边,可得![]() .所以原方程的解是
.所以原方程的解是![]() 或
或![]() .
.
例3:解不等式![]() .
.
在数轴上找出![]() 的解,即到1的距离为3的点对应的数为-2,4,如图,在-2的左边或在4的右边的
的解,即到1的距离为3的点对应的数为-2,4,如图,在-2的左边或在4的右边的![]() 值就满足
值就满足![]() ,所以
,所以![]() 的解为
的解为![]() 或
或![]() .
.
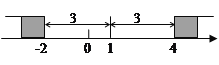
参考阅读材料,解答下列问题:
(1)方程![]() 的解为 ;
的解为 ;
(2)方程![]() 的解为 ;
的解为 ;
(3)若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E、F分别是ABCD的边BC、AD上的点,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)若四边形AECF是菱形,且BC=10,∠BAC=90°,求BE的长.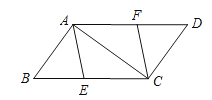
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com