
【题目】如图,已知在△ABC中,DE∥BC交AC于点E,交AB于点D,DE=![]() BC
BC
求证:D、E分别是AB、AC的中点.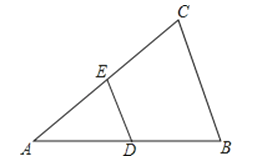
【答案】证明:作BF∥AC交ED的延长线于点F,
∵DE∥BC,
∴四边形BCEF是平行四边形,
∴BC=EF=2ED,AC∥BF,EC=BF,
∴ED=DF,∠A=∠DBF,
∴在△ADE与△BDF中,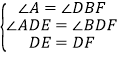 ,
,
∴△ADE≌△BDF(AAS)
∴AD=BD,AE=BF=EC,即D、E分别是AB、AC的中点.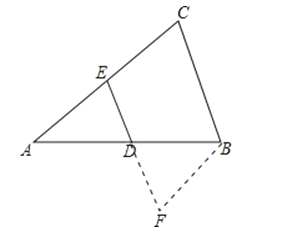
【解析】如图,作BF∥AC交ED的延长线于点F,构建平行四边形BCEF,利用平行四边形的性质和全等三角形的判定定理AAS得到△ADE≌△BDF,则该全等三角形的 对应边相等:AD=BD,AE=BF=EC,即证得结论.
【考点精析】本题主要考查了三角形中位线定理的相关知识点,需要掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图:在矩形ABCD中,AD=60cm,CD=120cm,E、F为AB边的三等分点,以EF为边在矩形内作等边三角形MEF,N为AB边上一点,EN=10cm;
请在矩形内找一点P,使△PMN为等边三角形(画出图形,并直接写出△PMF的面积).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点 ![]() 是双曲线
是双曲线 ![]() 在第三象限分支上的一个动点,连接
在第三象限分支上的一个动点,连接 ![]() 并延长交另一分支于点
并延长交另一分支于点 ![]() ,以
,以 ![]() 为边作等边三角形
为边作等边三角形 ![]() ,点
,点 ![]() 在第四象限内,且随着点
在第四象限内,且随着点 ![]() 的运动,点
的运动,点 ![]() 的位置也在不断变化,但点
的位置也在不断变化,但点 ![]() 始终在双曲线
始终在双曲线 ![]() 上运动,则
上运动,则 ![]() 的值是_______________.
的值是_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中,必然事件是( )
A.抛一枚硬币,正面朝上
B.打开电视频道,正在播放《今日视线》
C.射击运动员射击一次,命中10环
D.地球绕着太阳转
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】环境空气质量问题已经成为人们日常生活所关心的重要问题,我国新修订的《环境空气质量标准》中增加了PM2.5检测指标,“PM2.5”是指大气中危害健康的直径小于或等于2.5微米的颗粒物,2.5微米即0.0000025米.用科学记数法表示0.0000025为( )
A.2.5×10﹣5
B.2.5×105
C.2.5×10﹣6
D.2.5×106
查看答案和解析>>
科目:初中数学 来源: 题型:
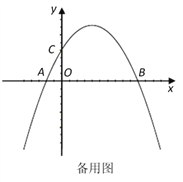
【题目】如图,在平面直角坐标系中,已知点A、B、C的坐标分别为(-1,0),(5,0),(0,2).
(1)求过A、B、C三点的抛物线解析式;
(2)若点P从A点出发,沿x轴正方向以每秒1个单位长度的速度向B点移动,连接PC并延长到点E,使CE=PC,将线段PE绕点P顺时针旋转90°得到线段PF,连接FB.若点P运动的时间为t秒(0≤t≤6),设△PBF的面积为S;
①求S与t的函数关系式;
②当t是多少时,△PBF的面积最大,最大面积是多少?
(3)点P在移动的过程中,△PBF能否成为直角三角形?若能,直接写出点F的坐标;若不能,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,菱形OABC的边OA在x轴正半轴上,OA=10,cos∠COA=![]() .一个动点P从点O出发,以每秒1个单位长度的速度沿线段OA方向运动,过点P作PQ⊥OA,交折线段OC﹣CB于点Q,以PQ为边向右作正方形PQMN,点N在射线OA上,当P点到达A点时,运动结束.设点P的运动时间为t秒(t>0).
.一个动点P从点O出发,以每秒1个单位长度的速度沿线段OA方向运动,过点P作PQ⊥OA,交折线段OC﹣CB于点Q,以PQ为边向右作正方形PQMN,点N在射线OA上,当P点到达A点时,运动结束.设点P的运动时间为t秒(t>0).
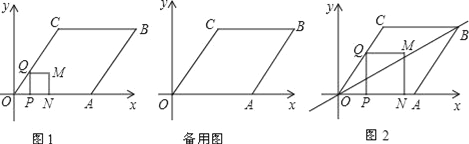
(1)C点的坐标为 ,当t= 时N点与A点重合;
(2)在整个运动过程中,设正方形PQMN与菱形OABC的重合部分面积为S,直接写出S与t之间的函数关系式和相应的自变量t的取值范围;
(3)如图2,在运动过程中,过点O和点B的直线将正方形PQMN分成了两部分,请问是否存在某一时刻,使得被分成的两部分中有一部分的面积是菱形面积的![]() ?若存在,请求出对应的t的值;若不存在,请说明理由.
?若存在,请求出对应的t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一件文化衫价格为18元,一个书包的价格比一件文化衫价格的2倍还少6元.
(1)求一个书包的价格是多少元?
(2)某公司出资1 800元,拿出不少于350元但不超过400元的经费奖励山区小学的优秀学生,剩余经费还能为多少名山区小学的学生每人购买一个书包和一件文化衫?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com