
【题目】如图,在△ABC中,若∠B=2∠C,AD⊥BC,E为BC边中点,求证:AB=2DE.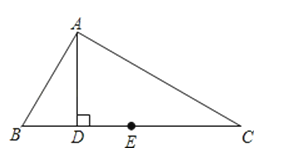
【答案】证明:取AC中点F,连接EF,DF,
则EF为中位线,且EF‖AB、∠FEC=∠B=2∠C,
在直角三角形ACD中,F是斜边AC的中点,
∴DF=CF,
∴∠DEF=∠C,
即有2∠FDC=∠FEC,
∴∠EFC=∠FDC+∠DFE,
∴2∠DFE=∠FEC=2∠FDC,
∴DE=EF,
∴AB=2DE.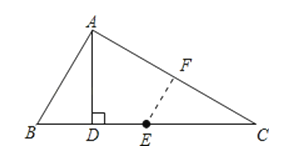
【解析】取AC中点F,连接EF、DF,则EF为△ABC的中位线,结合条件可得到∠FEC=2∠C,结合直角三角形的性质可得到∠EDF=∠EFD,得到DE=EF,可得出结论.
【考点精析】本题主要考查了三角形中位线定理的相关知识点,需要掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半才能正确解答此题.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】下列说法:(1)无限小数是无理数;(2)无理数都是带根号的数;(3)任何实数都可以开立方;(4)有理数都是实数.其中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
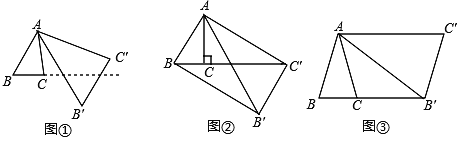
【题目】将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′ ,如图①所示,∠BAB′ =θ, ![]() ,我们将这种变换记为[θ,n] .
,我们将这种变换记为[θ,n] .
(1)如图①,对△ABC作变换[60°,![]() ]得到△AB′C′ ,则
]得到△AB′C′ ,则![]() :
:![]() = ;直线BC与直线B′C′所夹的锐角为 度;
= ;直线BC与直线B′C′所夹的锐角为 度;
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC作变换[θ,n]得到△AB′C′,使点B、C、![]() 在同一直线上,且四边形ABB′C′为矩形,求θ和n的值;
在同一直线上,且四边形ABB′C′为矩形,求θ和n的值;
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得到△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,求θ和n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校全体同学喜欢的NBA篮球明星的情况,小明抽取了七年级一班50名同学进行调查,得到最喜欢的NBA篮球明星的调查结果如下:
A A B C D A B A A C B A A C B C A A B C A A B A C
D B A C D B A C D A A B C D A C B A C A C D C A A
其中:A代表姚明,B代表科比,C代表詹姆斯,D代表麦迪.
填表:
明星 | 划记 | 人数 |
A | ||
B | ||
C | ||
D |
(2)该班同学喜欢最多的是谁?
(3)你认为小明所选取的样本是随机调查的样本吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
我们知道![]() 的几何意义是在数轴上数
的几何意义是在数轴上数![]() 对应的点与原点的距离;即
对应的点与原点的距离;即![]() ;这个结论可以推广为
;这个结论可以推广为![]() 表示在数轴上数
表示在数轴上数![]() ,
, ![]() 对应点之间的距离.绝对值的几何意义在解题中有着广泛的应用:
对应点之间的距离.绝对值的几何意义在解题中有着广泛的应用:
例1:解方程![]() .
.
容易得出,在数轴上与原点距离为4的点对应的数为±4,即该方程的![]() ±4;
±4;
例2:解方程![]() .
.
由绝对值的几何意义可知,该方程表示求在数轴上与-1和2的距离之和为5的点对应的![]() 的值.在数轴上,-1和2的距离为3,满足方程的
的值.在数轴上,-1和2的距离为3,满足方程的![]() 对应的点在2的右边或在-1的左边.若
对应的点在2的右边或在-1的左边.若![]() 对应的
对应的
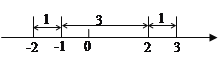
点在2的右边,如图可以看出![]() ;同理,若
;同理,若![]() 对应点在-1的左边,可得
对应点在-1的左边,可得![]() .所以原方程的解是
.所以原方程的解是![]() 或
或![]() .
.
例3:解不等式![]() .
.
在数轴上找出![]() 的解,即到1的距离为3的点对应的数为-2,4,如图,在-2的左边或在4的右边的
的解,即到1的距离为3的点对应的数为-2,4,如图,在-2的左边或在4的右边的![]() 值就满足
值就满足![]() ,所以
,所以![]() 的解为
的解为![]() 或
或![]() .
.
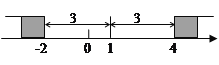
参考阅读材料,解答下列问题:
(1)方程![]() 的解为 ;
的解为 ;
(2)方程![]() 的解为 ;
的解为 ;
(3)若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com