
【题目】如图,在由边长为1个单位长度的小正方形组成的网格图中有格点△ABC.
(注:顶点在网格线交点处的三角形叫做格点三角形)
(1)图中AB的长为_________个单位长度;
(2)只用没有刻度的直尺,按如下要求画图:
① 以点C为位似中心,作△DEC∽△ABC,且相似比为1∶2;
②若点B为原点,点A(1,3),请在图2中画出平面直角坐标系,直接出△ABC的外心的坐标______________

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在2014年“元旦”前夕,某商场试销一种成本为30元的文化衫,经试销发现,若每件按34元的价格销售,每天能卖出36件;若每件按39元的价格销售,每天能卖出21件.假定每天销售件数y(件)是销售价格x(元)的一次函数.
(1)直接写出y与x之间的函数关系式.
(2)在不积压且不考虑其他因素的情况下,每件的销售价格定为多少元时,才能使每天获得的利润P最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC+BC=8,点O是斜边AB上一点,以O为圆心的⊙O分别与AC,BC相切于点D,E.

(1)当AC=2时,求⊙O的半径;
(2)设AC=x,⊙O的半径为y,求y与x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为将我们的城市装扮的更美丽,园林绿化工人要将公园一角的一块四边形的空地ABCD种植上花草.经测量,∠B=90°,AB=3米,BC=4米,CD=12米,DA=13米.若每平方米空地需要购买150元的花草.将这块空地全部绿化需要购买多少元的这种花草?
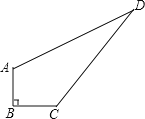
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD中,点Q是CD边的中点,过点Q作AQ⊥PQ交BC于P,(1)证明:△ADQ ∽△QCP;(2)若PC=1,求BP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:ABCD的对角线AC、BD相交于点O,过点D作DP∥OC且DP=OC,连接CP.得到四边形CODP.
(1)如图(1),在ABCD中,若∠ABC=90°,判断四边形CODP的形状,并证明;
(2)如图(2),在ABCD中,若AB=AD,判断四边形CODP的形状,并证明;
(3)如图(3),在ABCD中,若∠ABC=90°,且AB=AD,判断四边形CODP的形状,不需证明.
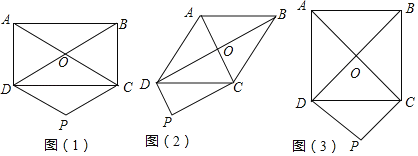
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于受到手机更新换代的影响,某手机店经销的甲品牌手机四月份售价比三月份每台降价500元.如果卖出相同数量的甲品牌手机,那么三月份销售额为9万元,四月份销售额只有8万元.
(1)四月份甲品牌手机每台售价为多少元?
(2)为了提高利润,该店计划五月份购进甲品牌及乙品牌手机销售,已知甲每台进价为3500元,乙每台进价为4000元,预算用不多于7.6万元且不少于7.5万元的资金购进这两种手机共20台,问按此预算要求,可以有几种进货方案,请写出所有进货方案?
(3)该店计划五月在销售甲品牌手机时,在四月份售价基础上每售出一台甲品牌手机再返还顾客现金![]() 元,而乙品牌手机按销售价4400元销售,如要使(2)中所有方案获利相同,
元,而乙品牌手机按销售价4400元销售,如要使(2)中所有方案获利相同,![]() 应取何值?
应取何值?
查看答案和解析>>
科目:初中数学 来源: 题型:
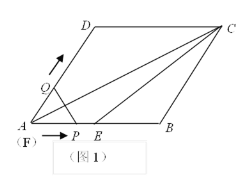
【题目】已知:如图1,菱形ABCD的边长为6,∠DAB=60°,点E是AB的中点,连接AC、EC.点Q从点A出发,沿折线A—D—C运动,同时点P从点A出发,沿射线AB运动,P、Q的速度均为每秒1个单位长度;以PQ为边在PQ的左侧作等边△PQF,△PQF与△AEC重叠部分的面积为S,当点Q运动到点C时P、Q同时停止运动,设运动的时间为t.
(1)当等边△PQF的边PQ恰好经过点D时,求运动时间t的值;当等边△PQF的边QF恰好经过点E时,求运动时间t的值;
(2)在整个运动过程中,请求出S与t之间的函数关系式和相应的自变量t的取值范围;
(3)如图2,当点Q到达C点时,将等边△PQF绕点P旋转α ° (0<α<360°),直线PF 分别与直线AC、直线CD交于点M、N.是否存在这样的α ,使△CMN为等腰三角形?若存在,请直接写出此时线段CM的长度;若不存在,请说明理由.
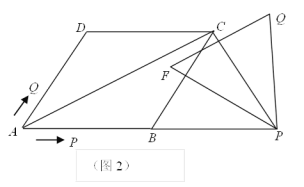
查看答案和解析>>
科目:初中数学 来源: 题型:
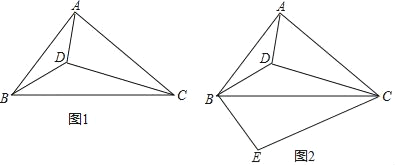
【题目】如图1,设D为锐角△ABC内一点,∠ADB=∠ACB+90°.
(1)求证:∠CAD+∠CBD=90°;
(2)如图2,过点B作BE⊥BD,BE=BD,连接EC,若ACBD=ADBC,
①求证:△ACD∽△BCE;
②求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com