
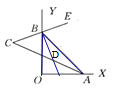
【题目】已知,如图,∠XOY=90°,点A、B分别在射线OX、OY上移动,BE是∠ABY的平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否发生变化?如果保持不变,请给出证明;如果随点A、B移动发生变化,请求出变化范围.

【答案】∠ACB的大小不发生变化,且始终保持45°.
【解析】
【试题分析】
作∠ABO的平分线交AC于点D,则∠BDA=180°-(∠DAB+∠DBA)=180°-![]() (∠OAB+∠OBA)=135°,由BD,BE分别是∠OBA和∠YBA的平分线,可知BD⊥CB,所以∠ACB=∠BDA-∠DBC=135°-90°=45°.可见∠ACB的大小始终为45°.
(∠OAB+∠OBA)=135°,由BD,BE分别是∠OBA和∠YBA的平分线,可知BD⊥CB,所以∠ACB=∠BDA-∠DBC=135°-90°=45°.可见∠ACB的大小始终为45°.
【试题解析】
作∠ABO的平分线交AC于点D,则∠BDA=180°-(∠DAB+∠DBA)=180°-![]() (∠OAB+∠OBA)=135°,因为BD,BE分别是∠OBA和∠YBA的平分线,
(∠OAB+∠OBA)=135°,因为BD,BE分别是∠OBA和∠YBA的平分线,
所以BD⊥CB,所以∠ACB=∠BDA-∠DBC=135°-90°=45°.
即∠ACB的大小始终为45°.


科目:初中数学 来源: 题型:
【题目】小东根据学习函数的经验,对函数y= ![]() 图象与性质进行了探究,下面是小东的探究过程,请补充完整,并解决相关问题:
图象与性质进行了探究,下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数y= ![]() 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)如表是y与x的几组对应值.
x | … | ﹣2 | ﹣1 | ﹣ | 0 | | 1 | | 2 | | 3 | 4 | … |
y | … | | | | 2 | | 4 | | 2 | | | m | … |
表中m的值为;
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出函数y= ![]() 的大致图象;
的大致图象; 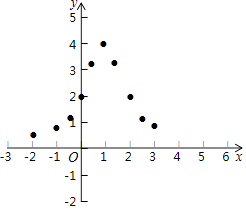
(4)结合函数图象,请写出函数y= ![]() 的一条性质.
的一条性质.
(5)解决问题:如果函数y= ![]() 与直线y=a的交点有2个,那么a的取值范围是 .
与直线y=a的交点有2个,那么a的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
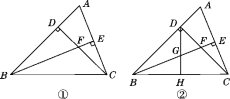
【题目】如图①,在等腰直角三角形BCD中,∠BDC=90°, BF平分∠DBC,与CD相交于点F,延长BD到A,使DA=DF.
(1)求证:△FBD≌△ACD;
(2)延长BF交AC于点E,且BE⊥AC,求证:CE=![]() BF;
BF;
(3)在(2)的条件下,H是BC边的中点,连接DH,与BE相交于点G,如图②. 试探索CE,GE,BG之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自动化车间计划生产480个零件,当生产任务完成一半时,停止生产进行自动化程序软件升级,用时20分钟,恢复生产后工作效率比原来提高了![]() ,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件?
,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=2,∠BAC=45°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D. 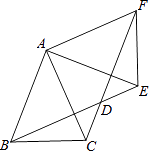
(1)求证:BE=CF;
(2)当四边形ABDF为菱形时,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“中秋”节前,朵朵的妈妈去超市购买了大小、形状、重量等都相同的五仁和豆沙月饼若干,放入不透明的盒中,此时从盒中随机取出五仁月饼的概率为 ![]() ;爸爸从盒中取出五仁月饼3只、豆沙粽子7只送给爷爷和奶奶后,这时随机取出五仁月饼的概率为
;爸爸从盒中取出五仁月饼3只、豆沙粽子7只送给爷爷和奶奶后,这时随机取出五仁月饼的概率为 ![]() .
.
(1)请你用所学知识计算:妈妈买的五仁月饼和豆沙月饼各有多少只?
(2)若朵朵一次从盒内剩余月饼中任取2只,问恰有五仁月饼、豆沙月饼各1只的概率是多少?(用列表法或树状图计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°.∠B′=110°,则∠BCA′的度数是( ) 
A.110°
B.80°
C.40°
D.30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com