
【题目】如图,△ABC中,AB=AC=2,∠BAC=45°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D. 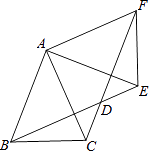
(1)求证:BE=CF;
(2)当四边形ABDF为菱形时,求CD的长.
【答案】
(1)证明:∵△AEF是由△ABC绕点A按逆时针方向旋转得到的,
∴AE=AF=AB=AC=2,∠EAF=∠BAC=45°,
∴∠BAC+∠3=∠EAF+∠3,即∠BAE=∠CAF,
在△ABE和△ACF中
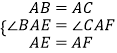 ,
,
∴△ABE≌△ACF,
∴BE=CF
(2)解:∵四边形ABDF为菱形,
∴DF=AF=2,DF∥AB,
∴∠1=∠BAC=45°,
∴△ACF为等腰直角三角形,
∴CF= ![]() AF=2
AF=2 ![]() ,
,
∴CD=CF﹣DF=2 ![]() ﹣2.
﹣2.
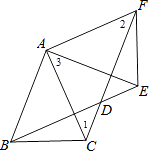
【解析】(1)根据旋转的性质得AE=AF=AB=AC=2,∠EAF=∠BAC=45°,然后根据“SAS”证明△ABE≌△ACF,于是根据全等三角形的性质即可得到结论;(2)根据菱形的性质得DF=AF=2,DF∥AB,再利用平行线的性质得∠1=∠BAC=45°,则可判断△ACF为等腰直角三角形,所以CF= ![]() AF=2
AF=2 ![]() ,然后计算CF﹣DF即可.
,然后计算CF﹣DF即可.
【考点精析】通过灵活运用菱形的性质和旋转的性质,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了即可以解答此题.


科目:初中数学 来源: 题型:
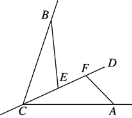
【题目】如图,已知CA=CB,点E,F在射线CD上,满足∠BEC=∠CFA,且∠BEC+∠ECB+∠ACF=180°.
(1)求证:△BCE≌△CAF;
(2)试判断线段EF,BE,AF的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BC=6 cm,AC=8 cm,将△BCD沿BD折叠,使点C落在AB边的C′点处,那么△ADC′的面积是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,∠XOY=90°,点A、B分别在射线OX、OY上移动,BE是∠ABY的平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否发生变化?如果保持不变,请给出证明;如果随点A、B移动发生变化,请求出变化范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】徐州至北京的高铁里程约为700km,甲、乙两人从徐州出发,分别乘坐“徐州号”高铁A与“复兴号”高铁B前往北京.已知A车的平均速度比B车的平均速度慢80km/h,A车的行驶时间比B车的行驶时间多40%,两车的行驶时间分别为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正比例函数y1=k1x(k1>0)与反比例函数y2= ![]() (k2>0)部分图象如图所示,则不等式k1x>
(k2>0)部分图象如图所示,则不等式k1x> ![]() 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)已知△ABC是等边三角形,点D是直线BC上一点,以AD为一边在AD的右侧作等边△ADE.
(1)如图①,点D在线段BC上移动时,直接写出∠BAD和∠CAE的大小关系;
(2)如图②,点D在线段BC的延长线上移动时,猜想∠DCE的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点A(2,0)的两条直线![]() ,
,![]() 分别交
分别交![]() 轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=
轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=![]() .
.

(1)求点B的坐标;
(2)若△ABC的面积为4,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距_____千米.
(2)走了一段路后,自行车发生故障进行修理,所用的时间是____小时.
(3)B出发后_____小时与A相遇.
(4)求出A行走的路程S与时间t的函数关系式.(写出计算过程)
(5)请通过计算说明:若B的自行车不发生故障,保持出发时的速度前进,何时与A相遇?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com