
【题目】如图,在Rt△ABC中,∠C=90°,BC=6 cm,AC=8 cm,将△BCD沿BD折叠,使点C落在AB边的C′点处,那么△ADC′的面积是________.

【答案】6 cm2
【解析】
试题先根据勾股定理得到AB=10cm,再根据折叠的性质得到DC=DC′,BC=BC′=6cm,则AC′=4cm,设DC=xcm,在Rt△ADC′中根据勾股定理列方程求得x的值,然后根据三角形的面积公式计算即可.
∵∠C=90°,BC=6cm,AC=8cm,
∴AB=10cm,
∵将△BCD沿BD折叠,使点C落在AB边的C′点,
∴△BCD≌△BC′D,
∴∠C=∠BC′D=90°,DC=DC′,BC=BC′=6cm,
∴AC′=AB-BC′=4cm,
设DC=xcm,则AD=(8-x)cm,
在Rt△ADC′中,AD2=AC′2+C′D2,
即(8-x)2=x2+42,解得x=3,
∵∠AC′D=90°,
∴△ADC′的面积═![]() ×AC′×C′D=
×AC′×C′D=![]() ×4×3=6(cm2).
×4×3=6(cm2).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB. 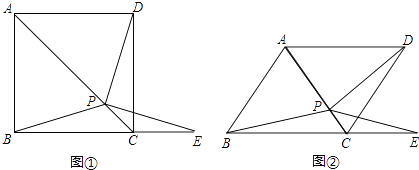
(1)求证:△BCP≌△DCP;
(2)求证:∠DPE=∠ABC;
(3)把正方形ABCD改为菱形,其它条件不变(如图②),若∠ABC=58°,则∠DPE=度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小东根据学习函数的经验,对函数y= ![]() 图象与性质进行了探究,下面是小东的探究过程,请补充完整,并解决相关问题:
图象与性质进行了探究,下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数y= ![]() 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)如表是y与x的几组对应值.
x | … | ﹣2 | ﹣1 | ﹣ | 0 | | 1 | | 2 | | 3 | 4 | … |
y | … | | | | 2 | | 4 | | 2 | | | m | … |
表中m的值为;
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出函数y= ![]() 的大致图象;
的大致图象; 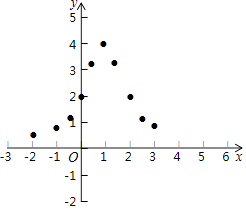
(4)结合函数图象,请写出函数y= ![]() 的一条性质.
的一条性质.
(5)解决问题:如果函数y= ![]() 与直线y=a的交点有2个,那么a的取值范围是 .
与直线y=a的交点有2个,那么a的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在等腰直角三角形BCD中,∠BDC=90°, BF平分∠DBC,与CD相交于点F,延长BD到A,使DA=DF.
(1)求证:△FBD≌△ACD;
(2)延长BF交AC于点E,且BE⊥AC,求证:CE=![]() BF;
BF;
(3)在(2)的条件下,H是BC边的中点,连接DH,与BE相交于点G,如图②. 试探索CE,GE,BG之间的数量关系,并证明你的结论.
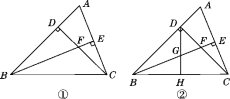
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=2,∠BAC=45°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D. 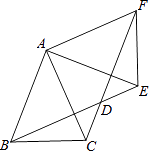
(1)求证:BE=CF;
(2)当四边形ABDF为菱形时,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⑴ 阅读理解:我们知道在直角三角形中,有无数组勾股数,例如:5、12、13;9、40、41;……但其中也有一些特殊的勾股数,例如:3、4、5;是三个连续正整数组成的勾股数.
解决问题:① 在无数组勾股数中,是否存在三个连续偶数能组成勾股数?
答: ,若存在,试写出一组勾股数: .
② 在无数组勾股数中,是否还存在其它的三个连续正整数能组成勾股数?若存在,求出勾股数,若不存在,说明理由.
③ 在无数组勾股数中,是否存在三个连续奇数能组成勾股数?若存在,求出勾股数,若不存在,说明理由.
⑵ 探索升华:是否存在锐角△ABC三边也为连续正整数;且同时还满足:∠B>∠C>∠A;∠ABC=2∠BAC?若存在,求出△ABC三边的长;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com