练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    用配方法解方程x2﹣4x+1=0时，配方后所得的方程是（　　）

    A．（x﹣2）2=1     B．（x﹣2）2=﹣1  C．（x﹣2）2=3     D．（x+2）2=3


    C【考点】解一元二次方程-配方法．

    【分析】此题考查了配方法解一元二次方程，“配方”一步．

    【解答】解：x2﹣4x+1=0

    移项得，x2﹣4x=﹣1，

    两边加4得，x2﹣4x+4=﹣1+4，

    即：（x﹣2）2=3．

    故选C．

    【点评】此题最重要的一步是在等式两边同时加上一次项系数一半的平方．

    　


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    下列条件中，不能得到等边三角形的是(     )

    A．有两个内角是60°的三角形

    B．三边都相等的三角形

    C．有一个角是60°的等腰三角形

    D．有两个外角相等的等腰三角形

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列说法中，正确的是（　　）

    A．为检测我市正在销售的酸奶质量，应该采用抽样调查的方式

    B．两名同学连续五次数学测试的平均分相同，方差较大的同学数学成绩更稳定

    C．抛掷一个正方体骰子，点数为奇数的概率是

    D．“打开电视，正在播放广告”是必然事件

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    解不等式组：．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


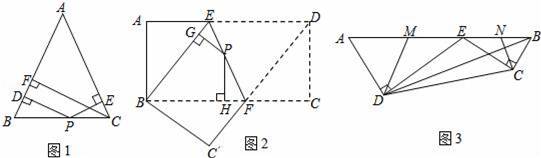
    【问题情境】如图1，在△ABC中，AB=AC，点P为边BC上的任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D、E，过点C作CF⊥AB，垂足为F．求证：PD+PE=CF．

    【结论运用】如图2，将矩形ABCD沿EF折叠，使点D落在点B上，点C落在点C′处，点P为折痕EF上的任一点，过点P作PG⊥BE、PH⊥BC，垂足分别为G、H，若AD=8，CF=3，求PG+PH的值；

    【迁移拓展】图3是一个航模的截面示意图．在四边形ABCD中，E为AB边上的一点，

    ED⊥AD，EC⊥CB，垂足分别为D、C，且AD•CE=DE•BC，AB=8，AD=3，BD=7；M、N分别为AE、BE的中点，连接DM、CN，求△DEM与△CEN的周长之和．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如果关于x的方程3x2﹣mx+3=0有两个相等的实数根，那么m的值为　　　　　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：6tan230°﹣2sin60°﹣2cos45°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知不等式组的解集是x≥2，则(     )

    A．a＜2  B．a=2   C．a＞2  D．a≤2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    二次函数y=ax2+bx+c（a为常数，且a≠0）的图象过点A（0，1），B（1，﹣2）和C（3，﹣2）．

    （1）求二次函数表达式；

    （2）若m＞n＞2，比较m2﹣4m与n2﹣4n的大小；

    （3）将抛物线y=ax2+bx+c平移，平移后图象的顶点为（h，k），若平移后的抛物线与直线y=x﹣1有且只有一个公共点，请用含h的代数式表示k．

    查看答案和解析>>

    同步练习册答案