
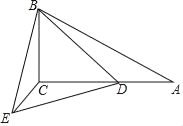
【题目】在Rt△ABC中,∠A=30°,∠ACB=90°,AB=10,D为AC上点.将BD绕点B顺时针旋转60°得到BE,连接CE.
(1)证明:∠ABD=∠CBE;
(2)连接ED,若ED=2![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)根据三角形的内角和得到∠ABC=60°,根据旋转的性质得到∠EBD=60°,根据角的和差即可得到∠ABD=∠CBE;
(2)过D作DH⊥AB于H,解直角三角形得到AD=2DH,AH=![]() DH,求得BH=10﹣
DH,求得BH=10﹣![]() DH,推出△BDE是等边三角形,得到BD=DE=2
DH,推出△BDE是等边三角形,得到BD=DE=2![]() ,根据勾股定理列方程即可得到结论.
,根据勾股定理列方程即可得到结论.
(1)∵在Rt△ABC中,∠A=30°,∠ACB=90°,
∴∠ABC=60°,
∵将BD绕点B顺时针旋转60°得到BE,
∴∠EBD=60°,
∴∠ABD=60°﹣∠CBD,∠CBE=60°﹣∠CBD,
∴∠ABD=∠CBE;
(2)过D作DH⊥AB于H,
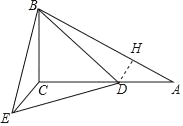
∵∠A=30°,
∴AD=2DH,AH=![]() DH,
DH,
∴BH=10﹣![]() DH,
DH,
∵将BD绕点B顺时针旋转60°得到BE,
∴BE=BD,
∴△BDE是等边三角形,
∴BD=DE=2![]() ,
,
在Rt△BDH中,BD2=BH2+DH2,
即(2![]() )2=(10﹣
)2=(10﹣![]() DH)2+DH2,
DH)2+DH2,
解得:DH=![]() ,或DH=4
,或DH=4![]() (不合题意舍去),
(不合题意舍去),
∴AD=2![]() ,
,
∵AC=5![]() ,
,
∴CD=3![]() ,
,
∴![]() =
=![]() .
.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
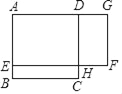
【题目】我县在治理违建的过程中,某小区拆除了自建房,改建绿地.如图,自建房占地是边长为20m的正方形ABCD,改建的绿地是矩形AEFG,其中点E在AB上,点G在AD的延长线上,且DG=2BE.如果设BE的长为x(单位:m),绿地AEFG的面积为y(单位:m2),那么y与x的函数的解析式为_____,绿地AEFG的最大面积为______m2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将函数y=![]() (x-2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A′,B′,若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是__________.
(x-2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A′,B′,若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
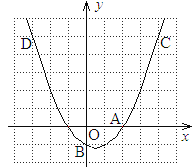
【题目】(已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b>0;③b2﹣4ac>0;④a﹣b+c>0,其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象过A(2,0),B(0,-1)和C(4,5)三点。
的图象过A(2,0),B(0,-1)和C(4,5)三点。
(1)求二次函数的解析式;
(2)设二次函数的图象与![]() 轴的另一个交点为D,求点D的坐标;
轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线![]() ,并写出当
,并写出当![]() 在什么范围内时,一次函数的值大于二次函数的值。
在什么范围内时,一次函数的值大于二次函数的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两校分别有一男一女共4名教师报名到农村中学支教.
(1)若从甲、乙两校报名的教师中分别随机选1名,则所选的2名教师性别相同的概率是 .
(2)若从报名的4名教师中随机选2名,用列表或画树状图的方法求出这2名教师来自同一所学校的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于钝角α,定义它的三角函数值如下:sinα=sin (180°-α),cosα=-cos (180°-α);若一个三角形的三个内角的比是1∶1∶4,A,B是这个三角形的两个顶点,sinA,cosB是方程4x2-mx-1=0的两个不相等的实数根,求m的值及∠A和∠B的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为2,弦BC的长为![]() ,点A为弦BC所对优弧上任意一点(B,C两点除外).
,点A为弦BC所对优弧上任意一点(B,C两点除外).
 (1)求∠BAC的度数;
(1)求∠BAC的度数;
(2)求△ABC面积的最大值.
(参考数据:![]() ,
,![]() ,
,![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
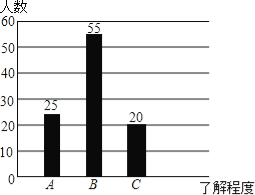
【题目】阳光中学组织学生开展社会实践活动,调查某社区居民对消防知识的了解程度(A:特别熟悉,B:有所了解,C:不知道),在该社区随机抽取了100名居民进行问卷调查,将调查结果制成如图所示的统计图,根据统计图解答下列问题:
(1)若该社区有居民900人,试估计对消防知识“特别熟悉”的居民人数;
(2)该社区的管理人员有男、女个2名,若从中选2名参加消防知识培训,试用列表或画树状图的方法,求恰好选中一男一女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com