【题目】（已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论：①abc＞0；②2a+b＞0；③b2﹣4ac＞0；④a﹣b+c＞0，其中正确的个数是（ ）
A. 1 B. 2 C. 3 D. 4
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，已知点A（﹣4，2），B（﹣1，﹣2），平行四边形ABCD的对角线交于坐标原点O．
（1）请直接写出点C、D的坐标；
（2）写出从线段AB到线段CD的变换过程；
（3）求△AOB的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某水产养殖户进行小龙虾养殖．已知每千克小龙虾养殖成本为6元，在整个销售旺季的80天里，销售单价p(元/千克)与时间第t(天)之间的函数关系为：
p＝
，日销售量y(千克)与时间第t(天)之间的函数关系如图所示．
(1)求日销售量y与时间t的函数解析式；
(2)哪一天的日销售利润最大？最大利润是多少？
(3)该养殖户有多少天日销售利润不低于2 400元？
(4)在实际销售的前40天中，该养殖户决定每销售1千克小龙虾，就捐赠m(m＜7)元给村里的特困户．在这前40天中，每天扣除捐赠后的日销售利润随时间t的增大而增大，求m的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
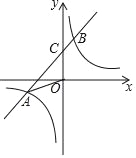
【题目】如图，一次函数y=kx+b（k≠0）的图象与反比例函数y=
（m≠0）的图象相交于点A（﹣3，﹣1）和点B，与y轴交于点C，△OAC的面积为3．
（1）求反比例函数的解析式；
（2）求一次函数的解析式，并写出点B的坐标；
（3）连接BO并延长交双曲线的另一支于点E，将直线y=kx+b向下平移a （a＞0）个单位长度后恰好经过点E，求a的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】春秋旅行社为吸引市民组团去天水湾风景区旅游，推出了如下收费标准：
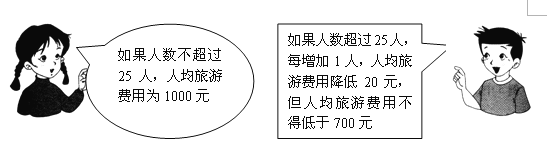某单位组织员工去天水湾风景区旅游，共支付给春秋旅行社旅游费用27000元，请问该单位这次共有多少员工去天水湾风景区旅游？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】列方程解下列实际问题
某校为美化校园，计划对面积为1800
的区域进行绿化，安排甲、乙两个工程队完成.已知甲队每天完成绿化的面积是乙队每天完成绿化面积的2倍，并且在独立完成面积为400区域的绿化时，甲队比乙队少用4天.求甲、乙两工程队每天能完成绿化的面积分别是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点，交y轴于点C，直线BC的表达式为y=﹣x+3．
（1）求抛物线的表达式；
（2）在直线BC上有一点P，使PO+PA的值最小，求点P的坐标；
（3）在x轴上是否存在一点Q，使得以A、C、Q为顶点的三角形与△BCD相似？若存在，请求出点Q的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在
中，
、
分别是
、
边上的点，
、
、
、…、
是
边的
等分点，
，
．如图1，若
，
，则
__________度；如图2，若
，
，则 __________（用含
，
的式子表示）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC与△A′B′C′成中心对称，下列说法不正确的是( )
A. S△ABC＝S△A′B′C′ B. AB＝A′B′，AC＝A′C′，BC＝B′C′
C. AB∥A′B′，AC∥A′C′，BC∥B′C′ D. S△ACO＝S△A′B′O
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
