
 如图,?ABCD的对角线AC、BD相交于点O,点E、F分别是线段AO、BO的中点,若EF=3,△OAB的周长是14,则AC+BD=16.
如图,?ABCD的对角线AC、BD相交于点O,点E、F分别是线段AO、BO的中点,若EF=3,△OAB的周长是14,则AC+BD=16. 分析 根据已知条件可以得到EF是△OAB的中位线,则AB=2EF=6.然后结合三角形的周长公式可以得到OA+OB=8;最后结合平行四边形的对角线相互平分可以得到AC+BD=2(OA+OB).
解答  解:如图,∵点E、F分别是线段AO、BO的中点,
解:如图,∵点E、F分别是线段AO、BO的中点,
∴EF是△OAB的中位线,
∴AB=2EF.
又∵EF=3,
∴AB=6.
∵△OAB的周长是14,
∴AB+OA+OB=14,即6+OA+OB=14,
∴OA+OB=8.
又∵四边形ABCD是平行四边形,
∴AC=2OA,BD=2OB.
∴AC+BD=2(OA+OB)=16.
故答案是:16.
点评 本题考查了三角形的中位线定理,解答本题需要用到:平行四边形的对角线互相平分,三角形中位线的判定定理及性质.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①b2-4ac>0;②abc<0;③a-b>0;④m>2,其中正确结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:①b2-4ac>0;②abc<0;③a-b>0;④m>2,其中正确结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 通常温度降到0℃以下,纯净的水结冰 | |
| B. | 随意翻到一本书的某页,这页的页码是奇数 | |
| C. | 掷一枚普通正方体骰子,向上的一面是7点 | |
| D. | 测量某天的最低气温,结果为-150℃ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
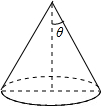 如图,已知圆锥的底面半径为5,侧面积为65π,设圆锥的母线与高的夹角为θ,则cosθ的值是( )
如图,已知圆锥的底面半径为5,侧面积为65π,设圆锥的母线与高的夹角为θ,则cosθ的值是( )| A. | $\frac{5}{12}$ | B. | $\frac{5}{13}$ | C. | $\frac{10}{13}$ | D. | $\frac{12}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | … | -2 | -1 | 0 | 1 | … |
| y | … | 0 | 4 | 6 | 6 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
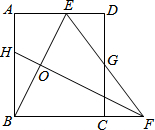 如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,以下几个结论:
如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,以下几个结论:| A. | ①③ | B. | ②③④ | C. | ①② | D. | ①②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com