
 如图,边长为2的正方形ABCD中,BD为对角线.AE∥BD,且DE=DB,DE与AB交于点F,则AE=
如图,边长为2的正方形ABCD中,BD为对角线.AE∥BD,且DE=DB,DE与AB交于点F,则AE=| 2 |
| 22+22 |
| 2 |
| 2 |
| 2 |
| 2 |
| 6 |
| 2 |
| 6 |
| 2 |
| 6 |
| 2 |


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 数学活动课上老师让学生以小组为单位测量学校旗杆AB的高度,如图所示,“希望小组”在教学楼一楼地面D处测得旗杆顶部仰角为60°,在教学楼三楼地面C处测得旗杆顶部仰角为30°,已知旗杆底部于教学楼一楼地面在同一水平线上,每层楼高为3米,求旗杆AB高度.
数学活动课上老师让学生以小组为单位测量学校旗杆AB的高度,如图所示,“希望小组”在教学楼一楼地面D处测得旗杆顶部仰角为60°,在教学楼三楼地面C处测得旗杆顶部仰角为30°,已知旗杆底部于教学楼一楼地面在同一水平线上,每层楼高为3米,求旗杆AB高度.查看答案和解析>>
科目:初中数学 来源: 题型:
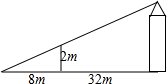 如图,为了测量一水塔的高度,小强用2米的竹竿做测量工具,移动竹竿,使竹竿、水塔的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8米,与水塔相距32米,则水塔的高度为
如图,为了测量一水塔的高度,小强用2米的竹竿做测量工具,移动竹竿,使竹竿、水塔的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8米,与水塔相距32米,则水塔的高度为查看答案和解析>>
科目:初中数学 来源: 题型:
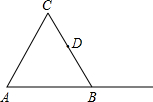 如图,△ABC是等边三角形,D是BC的中点.
如图,△ABC是等边三角形,D是BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com