
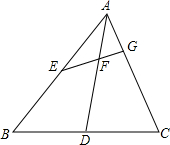
 在△ABC中,D、E分别为BC、AB的中点,EG⊥AC于点G,EG、AD交于点F,若AG=4,BC=2$\sqrt{29}$,tan∠DAC=$\frac{1}{2}$,则AC=12.
在△ABC中,D、E分别为BC、AB的中点,EG⊥AC于点G,EG、AD交于点F,若AG=4,BC=2$\sqrt{29}$,tan∠DAC=$\frac{1}{2}$,则AC=12. 分析 设AC=2a,连接DE,过D作DH⊥AC于H,根据D、E分别为BC、AB的中点,于是得到DE=$\frac{1}{2}$AC=a,DE∥AC,CD=$\frac{1}{2}BC$=$\sqrt{29}$,根据已知条件tan∠DAC=$\frac{FG}{AG}=\frac{FG}{4}$=$\frac{1}{2}$,求得FG=2,通过△AGF∽△DFE,根据相似三角形的性质得到$\frac{AG}{DE}=\frac{FG}{EF}$,求得EF=$\frac{1}{2}$a,得到DH=EH=2+$\frac{1}{2}$a,HC=2a-4-a=a-4,根据勾股定理列方程$(\frac{1}{2}a+2)^{2}+(a-4)^{2}=29$,即可得到结论.
解答 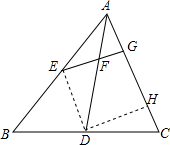 解:设AC=2a,连接DE,过D作DH⊥AC于H,
解:设AC=2a,连接DE,过D作DH⊥AC于H,
∵D、E分别为BC、AB的中点,
∴DE=$\frac{1}{2}$AC=a,DE∥AC,CD=$\frac{1}{2}BC$=$\sqrt{29}$,
∵tan∠DAC=$\frac{FG}{AG}=\frac{FG}{4}$=$\frac{1}{2}$,
∴FG=2,
∵DE∥AC,
∴△AGF∽△DFE,
∴$\frac{AG}{DE}=\frac{FG}{EF}$,
即$\frac{4}{a}=\frac{2}{EF}$,
∴EF=$\frac{1}{2}$a,
∴DH=EH=2+$\frac{1}{2}$a,HC=2a-4-a=a-4,
在Rt△DHC中,
DH2+CH2=DC2,
即$(\frac{1}{2}a+2)^{2}+(a-4)^{2}=29$,
解得:a=6,a=-$\frac{6}{5}$(舍去),
∴AC=12.
故答案为:12.
点评 本题考查了相似三角形的判定和性质,勾股定理,三角形的中位线的性质,正确的周长辅助线是解题的关键.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:解答题
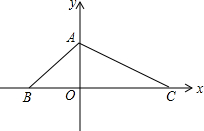 如图,已知,在平面直角坐标系中,S△ABC=24,OA=OB,BC=12.
如图,已知,在平面直角坐标系中,S△ABC=24,OA=OB,BC=12.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 有害污染物 | 排放量 | 占市区道路行驶机动车(含摩托车) 排放有害污染物总量 |
| 一氧化碳 | 11342吨 | 50% |
| 氮氧化物 | 2380吨 | |
| 非甲烷烃 | 2044吨 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com