
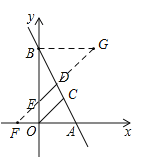
����Ŀ����ͼ1��ֱ��AB�ֱ���x�ᡢy�ύ��A��B���㣬OCƽ�֡�AOB��AB�ڵ�C����DΪ�߶�AB��һ�㣬����D��DE��OC��y���ڵ�E����֪AO��m��BO��n����m��n����n2��8n+16+|n��2m|��0��

��1����A��B��������ꣻ
��2������DΪAB�е㣬��OE�ij���
��3����ͼ2������P��x����2x+4��Ϊֱ��AB��x���·���һ�㣬��E��y�����������һ���㣬��EΪֱ�Ƕ���������ֱ����PEF��ʹ��F�ڵ�һ���ޣ���F��ĺᡢ������ʼ����ȣ����P�����꣮
���𰸡���1����AΪ��2��0������BΪ��0��4������2��OE��1����3����PΪ��4����4��
��������
��1�����ݷǸ��������ʣ��ó����̣�n��4��2+|n��2m|��0�����m��2��n��4�����ɵõ�A��B��������ꣻ
��2���ӳ�DE��x���ڵ�F���ӳ�FD����G��ʹ��DG��DF������BG������ȫ�������Σ��ٸ���BG=BE=AF�г�����x�ķ��̣��������OE�ij���
��3���ֱ����F��P��FM��y���ڵ�M��PN��y���ڵ�N�����EΪ��0��m��������ȫ�������Σ��ٸ���F��ĺ���������������ȣ��ó�����m+2x��4��m+x����ã�x=4�����ɵõ���PΪ��4��-4����
�⣺��1����n2��8n+16+|n��2m|��0��
�ࣨn��4��2+|n��2m|��0��
�ߣ�n��4��2��0��|n��2m|��0��
�ࣨn��4��2��0��|n��2m|��0��
��m��2��n��4��
���A��2��0������B��0��4����
��2���ӳ�DE��x���ڵ�F���ӳ�FD����G��ʹ��DG��DF������BG��
��OE��x��
��OCƽ�֡�AOB��
���BOC����AOC��45����
��DE��OC��
���EFO����FEO����BEG����BOC����AOC��45����
��OE��OF��x��
����ADF����BDG��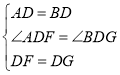 ��
��
���ADF�ա�BDG��SAS����
��BG��AF��2+x����G����AFE��45����
���G����BEG��45��
��BG��BE��4��x
��4��x��2+x��
��ã�x��1����OE��1��
��3���ֱ����F��P��FM��y���ڵ�M��PN��y���ڵ�N��
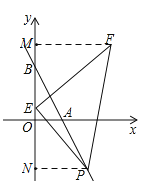
���E��0��m����
�ߵ�P������Ϊ��x����2x+4����
��PN��x��EN��m+2x��4��
�ߡ�PEF��90����
���PEN+��FEM��90����
��FM��y�ᣬ
���MFE+��FEM��90����
���PEN����MFE��
����EFM����PEN��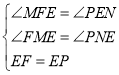 ��
��
���EFM�ա�PEN��AAS����
��ME��NP��x��FM��EN��m+2x��4��
���F��m+2x4��m+x����
��F��ĺ���������������ȣ�
��m+2x��4��m+x��
��ã�x��4��
���P��4����4����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������ҹ��Ŵ���ѧ�ľ���������������һ�����⣺�����лƽ��ö������һʮһö����֮���ʵȣ�������һ������ʮ�������ʽ���һö���ؼ��Σ�������˼�ǣ��״���װ�лƽ�9ö��ÿö�ƽ�������ͬ�����Ҵ���װ�а���11ö��ÿö����������ͬ��������������ȣ��������ཻ��1ö�״����Ҵ�����13���������������Բ��ƣ����ʻƽ𡢰���ÿö���ض���������ÿö�ƽ���x����ÿö������y������������ã�������
A. ![]()
B. ![]()
C. ![]()
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �İ뾶Ϊ
�İ뾶Ϊ![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ϣ����ı���
�ϣ����ı���![]() �Ǿ��Σ���
�Ǿ��Σ���![]() ���ӻ�
���ӻ�![]() ��һ���㣬
��һ���㣬![]() ��
��![]() �ֱ���
�ֱ���![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() ����
����![]() ��
��![]() ʱ��
ʱ��![]() �ij���Ϊ�� ��
�ij����� ��

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�еĶ��κ���y��ax2+bx+cͼ���У��۲�ó��������������Ϣ��
��b��0 ��c��0������������СֵΪ��3����a��b+c��0������x1��x2��2ʱ��y1��y2��
(1)����Ϊ������ȷ�����ļ�����(д�����)
(2)������ȷ�������������������ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�E��AB�ߵ��е㣬��EC���۾���ABCD��ʹB�����ڵ�P�����ۺ�ΪEC������AP���ӳ�AP��CD��F�㣬����CP���ӳ�CP��AD��Q�㣮�������½��ۣ����ı���AECFΪƽ���ı��Σ��ڡ�PBA����APQ���ۡ�FPCΪ���������Σ��ܡ�APB�ա�EPC��������ȷ���۵ĸ���Ϊ( )

A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������ͬʱ��![]() �س���ǰ��
�س���ǰ��![]() �أ����м׳�ѡ���иܵ�·�ߣ�ȫ�̹�
�أ����м׳�ѡ���иܵ�·�ߣ�ȫ�̹�![]() ���ҳ�ѡ��û�иܵ�·�ߣ�ȫ�̹�
���ҳ�ѡ��û�иܵ�·�ߣ�ȫ�̹�![]() .�׳���ʻ��ƽ���ٶȱ��ҳ���ʻ��ƽ���ٶ�ÿСʱ��
.�׳���ʻ��ƽ���ٶȱ��ҳ���ʻ��ƽ���ٶ�ÿСʱ��![]() ǧ�ף��ҳ�����
ǧ�ף��ҳ�����![]() �ػ��ѵ�ʱ���Ǽ׳���
�ػ��ѵ�ʱ���Ǽ׳���![]() ��.�ʼס���������ʻ��ƽ���ٶȷֱ��Ƕ��٣�
��.�ʼס���������ʻ��ƽ���ٶȷֱ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ�κ���![]() ��ͼ����
��ͼ����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��һ�κ���
��һ�κ���![]() ��ͼ����
��ͼ����![]() �ύ�ڵ�
�ύ�ڵ�![]() ������
������![]() ���Լ�һ�κ���
���Լ�һ�κ���![]() ��ͼ��ֱ��ڵ�
��ͼ��ֱ��ڵ�![]() ��
��![]() ����
����![]() ������Ϊ
������Ϊ![]() .
.

��1������![]() ��
��![]() �ķ�����
�ķ�����![]() �Ľ�Ϊ______________.
�Ľ�Ϊ______________.
��2������![]() �IJ���ʽ
�IJ���ʽ![]() �Ľ⼯Ϊ__________________.
�Ľ⼯Ϊ__________________.
��3�����ı���![]() �������
�������
��4����![]() �����Ƿ���ڵ�
�����Ƿ���ڵ�![]() ��ʹ���Ե�
��ʹ���Ե�![]() ��
��![]() ��
��![]() Ϊ�������������ֱ�������Σ������ڣ������
Ϊ�������������ֱ�������Σ������ڣ������![]() �����꣺�������ڣ���˵������.
�����꣺�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�ǡ�ABC�����Բ��AEƽ�֡�BAC����O�ڵ�E����BC�ڵ�D������E��ֱ��l��BC��

��1���ж�ֱ��l���O��λ�ù�ϵ����˵�����ɣ�
��2������ABC��ƽ����BF��AD�ڵ�F����֤��BE=EF��
��3���ڣ�2���������£���DE=4��DF=3����AF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ý�屨�����ڵ�52�������¼�������ҹ���¼ѡ�ֻ����7ö���ơ�7ö���ƺ�4öͭ�ƣ��ڹ�����̨��չʾ��ָ���ϵġ��й��ٶȡ��������������ź�ѧ��С����С�����ܹ��裬��������ҵ��ʱ����ϰ���֣�����һ��ʱ���Ŭ�������ǵ�¼���ٶ��������Ե���ߣ�����������С����140��������ʱ����С����175��������ʱ����ͬ��С��ƽ��ÿ���ӱ�С���ٴ�15���֣������С��ƽ��ÿ���Ӵ��ֵĸ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com