练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】据媒体报道，在第52届国际速录大赛中我国速录选手获得了7枚金牌、7枚银牌和4枚铜牌，在国际舞台上展示了指尖上的“中国速度”．看到这则新闻后，学生小明和小海很受鼓舞，决定利用业余时间练习打字．经过一段时间的努力，他们的录入速度有了明显的提高．经测试现在小明打140个字所用时间与小海打175个字所用时间相同，小明平均每分钟比小海少打15个字．请求出小明平均每分钟打字的个数．

    【答案】小明平均每分钟打60个字.

    【解析】

    设小明平均每分钟打个字，则小海平均每分钟打个字,根据“小明打140个字所用时间与小海打175个字所用时间相同”列出分式方程，求解（并验证）即可.

    解：设小明平均每分钟打个字，则小海

    平均每分钟打个字.

    根据题意，得.

    解得 .

    经检验：是原方程的解，且符合题意.

    答：小明平均每分钟打60个字.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图1，直线AB分别与x轴、y轴交于A、B两点，OC平分∠AOB交AB于点C，点D为线段AB上一点，过点D作DE∥OC交y轴于点E，已知AO＝m，BO＝n，且m、n满足n2﹣8n+16+|n﹣2m|＝0．

    （1）求A、B两点的坐标；

    （2）若点D为AB中点，求OE的长；

    （3）如图2，若点P（x，﹣2x+4）为直线AB在x轴下方的一点，点E是y轴的正半轴上一动点，以E为直角顶点作等腰直角△PEF，使点F在第一象限，且F点的横、纵坐标始终相等，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，是的中点，是边上一动点，连结，取的中点，连结.小梦根据学习函数的经验，对的面积与的长度之间的关系进行了探究：

    （1）设的长度为，的面积，通过取边上的不同位置的点，经分析和计算，得到了与的几组值，如下表：

    0

    1

    2

    3

    4

    5

    6

    3

    1

    0

    2

    3

    根据上表可知，______，______.

    （2）在平面直角坐标系中，画出（1）中所确定的函数的图象.

    （3）在（1）的条件下，令的面积为.

    ①用的代数式表示.

    ②结合函数图象.解决问题：当时，的取值范围为______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，甲、乙两人在玩转盘游戏时，准备了两个可以自由转动的转盘A，B，每个转盘被分成面积相等的几个扇形，并在每一个扇形内标上数字．游戏规则：同时转动两个转盘，当转盘停止后，指针所指区域的数字之和为0时，甲获胜；数字之和为1时，乙获胜．如果指针恰好指在分割线上，那么重转一次，直到指针指向某一区域为止．

    （1）用画树状图或列表法求乙获胜的概率；

    （2）这个游戏规则对甲、乙双方公平吗？请判断并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2019年12月18日，新版《北京市生活垃圾管理条例》正式发布，并将在2020年5月1日起正式实施，这标志着北京市生活垃圾分类将正式步入法制化、常态化、系统化轨道．目前，相关配套设施的建设已经开启．如图，计划在某小区道路l上建一个智能垃圾分类投放点O，使得道路l附近的两栋住宅楼Ａ，B到智能垃圾分类投放点O的距离相等．

    （1）请在图中利用尺规作图（保留作图痕迹，不写作法），确定点O的位置；

    （2）确定点O位置的依据为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某航空公司经营A、B、C、D四个城市之间的客运业务．若机票价格y（元）是两城市间的距离x（千米）的一次函数．今年“五一”期间部分机票价格如下表所示：

    起点

    终点

    距离x（千米）

    价格y（元）

    A

    B

    1000

    2050

    A

    C

    800

    1650

    A

    D

    2550

    B

    C

    600

    C

    D

    950

    （1）求该公司机票价格y（元）与距离x（千米）的函数关系式；

    （2）利用（1）中的关系式将表格填完整；

    （3）判断A、B、C、D这四个城市中，哪三个城市在同一条直线上？请说明理由；

    （4）若航空公司准备从旅游旺季的7月开始增开从B市直接飞到D市的旅游专线，且按以上规律给机票定价，那么机票定价应是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】是等边三角形，点在射线上，延长至，使.

    （1）如图（1），当点为线段中点时，求证：.

    （2）如图（2），当点在线段的延长线上时，还成立吗？若成立，请给予证明；若不成立，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，E是正方形ABCD中CD边上一点，以点A为中心把△ADE顺时针旋转90°。

    （1）在图中画出旋转后的图形；

    （2）若旋转后E点的对应点记为M，点F在BC上，且∠EAF=45°，连接EF。

    ①求证：△AMF≌△AEF；

    ②若正方形的边长为6，AE＝，求EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在Rt△ABC与Rt△OCD中，∠ACB=∠DCO=90°，O为AB的中点．

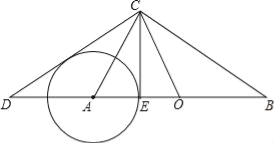
    （1）求证：∠B=∠ACD．

    （2）已知点E在AB上，且BC2=ABBE．

    （i）若tan∠ACD=，BC=10，求CE的长；

    （ii）试判定CD与以A为圆心、AE为半径的⊙A的位置关系，并请说明理由．

    查看答案和解析>>

    同步练习册答案