
【题目】如图,![]() 的半径为
的半径为![]() ,点
,点![]() 、
、![]() 、
、![]() 、
、![]() 在
在![]() 上,且四边形
上,且四边形![]() 是矩形,点
是矩形,点![]() 是劣弧
是劣弧![]() 上一动点,
上一动点,![]() 、
、![]() 分别与
分别与![]() 相交于点
相交于点![]() 、点
、点![]() .当
.当![]() 且
且![]() 时,
时,![]() 的长度为( )
的长度为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
作辅助线,构建矩形的对角线,根据等边对等角得∠ABP=∠APB,由同弧所对的圆周角相等可得∠ACB=∠ACP,进而得到AF=FC.根据矩形的四个角都是直角得∠ABC=90°,AE=EF=FD得FC=2FD,∠DCF=30°,得出∠ACB=30°,求出BC的长,AD的长,再三等分即可.
连接AC、BD.
∵PA=AB,∴∠ABP=∠APB.
∵∠ABP=∠ACP,∠APB=∠ACB,∴∠ACB=∠ACP.
∵AD∥BC,∴∠DAC=∠ACB,∴∠ACP=∠DAC,∴AF=FC.
∵AE=EF=FD,设FD=x,则FC=AF=2x.
∵四边形ABCD为矩形,∴AD=BC,∠ABC=∠ADC=90°,∴AC为⊙O的直径.
在Rt△DFC中,FC=2FD,∴∠DCF=30°,∴∠ACB=∠ACP=30°.
∵⊙O的半径为1,∴AC=2,∴AB=1,BC=![]() ,∴AD=BC=
,∴AD=BC=![]() .
.
∵AE=EF=FD,∴AE=![]() .
.


科目:初中数学 来源: 题型:
【题目】在初中阶段的函数学习中,我们经历了“确定函数的表达式——利用函数图象研究其性质——运用函数解决问题”的学习过程. 在画函数图象时,我们通过描点、平移、对称的方法画出了所学的函数图象. 同时,我们也学习了绝对值的意义![]() ,结合上面经历的学习过程,现在来解决下面的问题
,结合上面经历的学习过程,现在来解决下面的问题
在函数![]() 中,自变量
中,自变量![]() 的取值范围是全体实数,下表是
的取值范围是全体实数,下表是![]() 与
与![]() 的几组对应值:
的几组对应值:
|
| 0 | 1 | 2 | 3 | ||
y | … | 0 | 1 | 2 | 3 | 2 | … |
(1)根据表格填写:![]() _______.
_______.
(2)化简函数解析式:
当![]() 时,
时,![]() _______;
_______;
当![]() 时,
时,![]() ______.
______.
(3)在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象并解决以下问题;
①该函数的最大值为_______.
②若![]() 为该函数图象上不同的两点,则
为该函数图象上不同的两点,则![]() ________.
________.
③根据图象可得关于![]() 的方程
的方程![]() 的解为_______.
的解为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
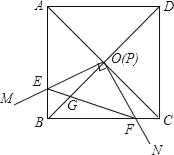
【题目】如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G.
(1)求四边形OEBF的面积;
(2)求证:OGBD=EF2;
(3)在旋转过程中,当△BEF与△COF的面积之和最大时,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为直线BC上一动点(不与点B,C重合),在AD的右侧作△ACE,使得AE=AD,∠DAE=∠BAC,连接CE.

(1)当D在线段![]() 上时.
上时.
①求证:![]() .
.
②请判断点D在何处时,![]() ,并说明理由.
,并说明理由.
(2)当![]() 时,若
时,若![]() 中最小角为28°,求
中最小角为28°,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是弦,点D是弧BC的中点,PD切⊙O于点D.
(1)求证:DP⊥AP;
(2)若PD=![]() ,PC=1,求图中阴影部分的面积.(结果保留π)
,PC=1,求图中阴影部分的面积.(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 在边
在边![]() 上,
上,![]() 在线段
在线段![]() 上,
上,![]() ,
,![]() 是等边三角形,边
是等边三角形,边![]() 交边
交边![]() 于点
于点![]() ,边
,边![]() 交边
交边![]() 于点
于点![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 当
当![]() 为何值时,以
为何值时,以![]() 为圆心,以
为圆心,以![]() 为半径的圆与
为半径的圆与![]() 相切?
相切?
![]() 设
设![]() ,五边形
,五边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数解析式(要求写出自变量
之间的函数解析式(要求写出自变量![]() 的取值范围);当
的取值范围);当![]() 为何值时,
为何值时,![]() 有最大值?并求
有最大值?并求![]() 的最大值.
的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线AB分别与x轴、y轴交于A、B两点,OC平分∠AOB交AB于点C,点D为线段AB上一点,过点D作DE∥OC交y轴于点E,已知AO=m,BO=n,且m、n满足n2﹣8n+16+|n﹣2m|=0.

(1)求A、B两点的坐标;
(2)若点D为AB中点,求OE的长;
(3)如图2,若点P(x,﹣2x+4)为直线AB在x轴下方的一点,点E是y轴的正半轴上一动点,以E为直角顶点作等腰直角△PEF,使点F在第一象限,且F点的横、纵坐标始终相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是边
是边![]() 上一动点,连结
上一动点,连结![]() ,取
,取![]() 的中点
的中点![]() ,连结
,连结![]() .小梦根据学习函数的经验,对
.小梦根据学习函数的经验,对![]() 的面积与
的面积与![]() 的长度之间的关系进行了探究:
的长度之间的关系进行了探究:

(1)设![]() 的长度为
的长度为![]() ,
,![]() 的面积
的面积![]() ,通过取
,通过取![]() 边上的不同位置的点
边上的不同位置的点![]() ,经分析和计算,得到了
,经分析和计算,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 |
| 1 | 0 |
| 2 | 3 |
根据上表可知,![]() ______,
______,![]() ______.
______.
(2)在平面直角坐标系![]() 中,画出(1)中所确定的函数的图象.
中,画出(1)中所确定的函数的图象.

(3)在(1)的条件下,令![]() 的面积为
的面积为![]() .
.
①用![]() 的代数式表示
的代数式表示![]() .
.
②结合函数图象.解决问题:当![]() 时,
时,![]() 的取值范围为______.
的取值范围为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com