
【题目】《张邱建算经》是中国古代数学史上的杰作,该书中有首古民谣记载了一数列问题:“南山一棵竹,竹尾风割断,剩下三十节,一节一个圈.头节高五寸① , 头圈一尺三② . 逐节多三分③ , 逐圈少分三④ . 一蚁往上爬,遇圈则绕圈.爬到竹子顶,行程是多远?”(注释:①第一节的高度为0.5尺;②第一圈的周长为1.3尺;③每节比其下面的一节多0.03尺;④每圈周长比其下面的一圈少0.013尺) 问:此民谣提出的问题的答案是( )
A.72.705尺
B.61.395尺
C.61.905尺
D.73.995尺
【答案】B
【解析】解:∵每竹节间的长相差0.03尺, 设从地面往长,每节竹长为a1 , a2 , a3 , …,a30 ,
∴{an}是以a1=0.5为首项,以d′=0.03为公差的等差数列,
由题意知竹节圈长,后一圏比前一圏细1分3厘,即0.013尺,
设从地面往上,每节节圈长为b1 , b2 , b3 , …,b30 ,
由{bn}是以b1=1.3为首项,d=﹣0.013为公差的等差数列,
∴一蚁往上爬,遇圈则绕圈.爬到竹子顶,行程是:
S30=(30×0.5+ ![]() ×0.03)+[30×1.3+
×0.03)+[30×1.3+ ![]() ×(﹣0013)]=61.395.
×(﹣0013)]=61.395.
故选:B.
设从地面往长,每节竹长为a1 , a2 , a3 , …,a30 , 则{an}是以a1=0.5为首项,以d′=0.03为公差的等差数列,设从地面往上,每节节圈长为b1 , b2 , b3 , …,b30 , 则{bn}是以b1=1.3为首项,d=﹣0.013为公差的等差数列,由此能求出一蚁往上爬,遇圈则绕圈.爬到竹子顶的行程.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线y= ![]() x上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=
x上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y= ![]() x上,依次进行下去…,若点A的坐标是(0,1),点B的坐标是(
x上,依次进行下去…,若点A的坐标是(0,1),点B的坐标是( ![]() ,1),则点A8的横坐标是 .
,1),则点A8的横坐标是 . 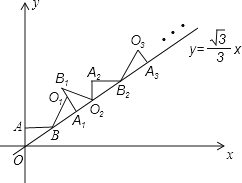
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过随机询问某地100名高中学生在选择座位时是否挑同桌,得到如下2×2列联表:
男生 | 女生 | 合计 | |
挑同桌 | 30 | 40 | 70 |
不挑同桌 | 20 | 10 | 30 |
总计 | 50 | 50 | 100 |
(Ⅰ)从这50名男生中按是否挑同桌采取分层抽样的方法抽取一个容量为5的样本,现从这5人中随机选取3人做深度采访,求这3名学生中至少有2名要挑同桌的概率;
(Ⅱ)根据以上2×2列联表,是否有95%以上的把握认为“性别与在选择座位时是否挑同桌”有关?
下面的临界值表供参考:
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知F1、F2分别为双曲线C: ![]() =1的左、右焦点,P为双曲线C右支上一点,且|PF1|=2|PF2|,则△PF1F2外接圆的面积为( )
=1的左、右焦点,P为双曲线C右支上一点,且|PF1|=2|PF2|,则△PF1F2外接圆的面积为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知椭圆E: ![]() =1(a>b>0)的左焦点F1(﹣
=1(a>b>0)的左焦点F1(﹣ ![]() ,0),若椭圆上存在一点D,满足以椭圆短轴为直径的圆与线段DF1相切于线段DF1的中点F
,0),若椭圆上存在一点D,满足以椭圆短轴为直径的圆与线段DF1相切于线段DF1的中点F
(1)求椭圆E的方程;
(2)过坐标原点O的直线交椭圆W: ![]() =1于P、A两点,其中点P在第一象限,过P作x轴的垂线,垂足为C,连结AC并延长交椭圆W于B,求证:PA⊥PB.
=1于P、A两点,其中点P在第一象限,过P作x轴的垂线,垂足为C,连结AC并延长交椭圆W于B,求证:PA⊥PB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( ) 
A.4.5
B.6
C.7.5
D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)求每套队服和每个足球的价格是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com