
【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°﹣∠ABD;④∠BDC=∠BAC.其中正确的结论有( ) 
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】解:①∵AD平分△ABC的外角∠EAC, ∴∠EAD=∠DAC,
∵∠EAC=∠ACB+∠ABC,且∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,
故①正确.
②由(1)可知AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABC=2∠ADB,
∵∠ABC=∠ACB,
∴∠ACB=2∠ADB,
故②正确.
③在△ADC中,∠ADC+∠CAD+∠ACD=180°,
∵CD平分△ABC的外角∠ACF,
∴∠ACD=∠DCF,
∵AD∥BC,
∴∠ADC=∠DCF,∠ADB=∠DBC,∠CAD=∠ACB
∴∠ACD=∠ADC,∠CAD=∠ACB=∠ABC=2∠ABD,
∴∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,
∴∠ADC+∠ABD=90°
∴∠ADC=90°﹣∠ABD,
故③正确;
④∵∠BAC+∠ABC=∠ACF,
∴ ![]() ∠BAC+
∠BAC+ ![]() ∠ABC=
∠ABC= ![]() ∠ACF,
∠ACF,
∵∠BDC+∠DBC= ![]() ∠ACF,
∠ACF,
∴ ![]() ∠BAC+
∠BAC+ ![]() ∠ABC=∠BDC+∠DBC,
∠ABC=∠BDC+∠DBC,
∵∠DBC= ![]() ∠ABC,
∠ABC,
∴ ![]() ∠BAC=∠BDC,即∠BDC=
∠BAC=∠BDC,即∠BDC= ![]() ∠BAC.
∠BAC.
故④错误.
故选C.
【考点精析】解答此题的关键在于理解平行线的判定的相关知识,掌握同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行,以及对三角形的“三线”的理解,了解1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内.


科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:
①abc>0
②4a+2b+c>0
③4ac﹣b2<8a
④![]() <a<
<a<![]()
⑤b>c.
其中含所有正确结论的选项是( )

A.①③ B.①③④ C.②④⑤ D.①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2). 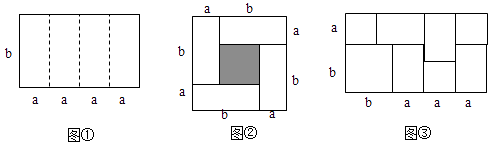
(1)图②中的阴影部分的面积为;
(2)观察图②请你写出 (a+b)2 , (a﹣b)2 , ab之间的等量关系是;
(3)根据(2)中的结论,若x+y=4,xy= ![]() ,则(x﹣y)2=;
,则(x﹣y)2=;
(4)实际上通过计算图形的面积可以探求相应的等式.如图③,你发现的等式是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①矩形是轴对称图形,两条对角线所在的直线是它的对称轴;②两条对角线相等的四边形是矩形;③有两个角相等的平行四边形是矩形;④两条对角线相等且互相平分的四边形是矩形;⑤两条对角线互相垂直平分的四边形是矩形.其中,正确的有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,不正确的是( )
A.三个角的度数之比为1:3:4的三角形是直角三角形
B.三个角的度数之比为3:4:5的三角形是直角三角形
C.三边长度之比为3:4:5的三角形是直角三角形
D.三边长度之比为9:40:41的三角形是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于y的一元二次方程ky2﹣2y﹣1=0有两个不相等的实数根,则k的取值范围是( )
A. k>﹣1 B. k>﹣1且k≠0 C. k<1 D. k<1 且k≠0
查看答案和解析>>
科目:初中数学 来源: 题型:
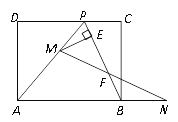
【题目】如图,已知矩形ABCD的一条边AD=8 cm,点P在CD边上,AP=AB, PC=4cm,连结PB.点M从点P出发,沿PA方向匀速运动(点M与点P、A不重合);点N同时从点B出发,沿线段AB的延长线匀速运动,连结MN交PB于点F.
(1)求AB的长;
(2)若点M的运动速度为1cm/s,点N的运动速度为2cm/s,△AMN的面积为S,点M和点N的运动时间为![]() ,求S与
,求S与![]() 的函数关系式,并求S的最大值;
的函数关系式,并求S的最大值;
(3)若点M和点N的运动速度相等,作ME⊥BP于点E.试问当点M、N在运动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com