
����Ŀ����ͼ����֪����ABCD��һ����AD=8 cm����P��CD���ϣ�AP=AB�� PC=4cm������PB����M�ӵ�P��������PA���������˶�����M���P��A���غϣ�����Nͬʱ�ӵ�B���������߶�AB���ӳ��������˶�������MN��PB�ڵ�F��
��1����AB�ij���
��2������M���˶��ٶ�Ϊ1cm/s����N���˶��ٶ�Ϊ2cm/s����AMN�����ΪS����M�͵�N���˶�ʱ��Ϊ![]() ����S��
����S��![]() �ĺ�����ϵʽ������S�����ֵ��
�ĺ�����ϵʽ������S�����ֵ��
��3������M�͵�N���˶��ٶ���ȣ���ME��BP�ڵ�E�����ʵ���M��N���˶������У��߶�EF�ij����Ƿ����仯�����仯��˵�����ɣ������䣬����߶�EF�ij��ȣ�
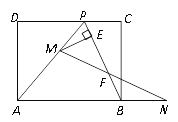
���𰸡���1��10����2��![]() ʱ��Sȡ�����ֵΪ45����3����M��N���˶������У��߶�EF�ij��Ȳ��䣬����Ϊ
ʱ��Sȡ�����ֵΪ45����3����M��N���˶������У��߶�EF�ij��Ȳ��䣬����Ϊ![]() ��
��
�������������������1����AB=x�������۵��ɵ�AP=CD=x��DP=CD-CP=x-4�����ù��ɶ�������Rt��ADP�У�AD2+DP2=AP2����82+��x-4��2=x2�����ɽ����2������M��MG��AN�ڵ�G�����AGM=��D��90�������ԡ�APD=��MAG����Rt��APD��Rt��MAG������![]() ����
����![]() ���ɵó�
���ɵó�![]() �� ����Ϊ
�� ����Ϊ![]() ������
������![]()
![]()
![]() ����
����![]() ʱ��Sȡ�����ֵΪ45����3����MQ��AN����PB�ڵ�Q�����MP=MQ��BN=QM���ó�MP=MQ������MH��PQ���ó�HQ=
ʱ��Sȡ�����ֵΪ45����3����MQ��AN����PB�ڵ�Q�����MP=MQ��BN=QM���ó�MP=MQ������MH��PQ���ó�HQ=![]() PQ�����ݡ�QMF=��BNF��֤����MFQ�ա�NFB���ó�QF=
PQ�����ݡ�QMF=��BNF��֤����MFQ�ա�NFB���ó�QF=![]() QB�������EF=
QB�������EF=![]() PB��������HF=
PB��������HF=![]() PB���ɵó��߶�EF�ij��Ȳ��䣻
PB���ɵó��߶�EF�ij��Ȳ��䣻
���������
��1����AB= ![]() ����AP=
����AP= ![]() ��DP=
��DP= ![]() ��
��
��Rt��ADP�У� �ɹ��ɶ����ã�
![]() ��
��
��ã� ![]() ��
��
��AB =10��
��2������M��MG��AN�ڵ�G�����AGM=��D��90����
��DC��AB��
���APD=��MAG��
��Rt��APD��Rt��MAG��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]()
![]()
![]()
�൱![]() ʱ��Sȡ�����ֵΪ45��
ʱ��Sȡ�����ֵΪ45��
��3����MQ��AN����PB�ڵ�Q��
��AP=AB��MQ��AN��
���APB=��ABP����ABP=��MQP��
���APB=��MQP��
��MP=MQ��
��ME��PQ��
��PE=EQ=![]() PQ��
PQ��
��BN=PM��PM=MQ��
��BN=QM��
��MQ��AN�����QMF=��BNF��
����MFQ����NFB��
��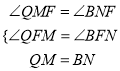 ��
��
���MFQ�ա�NFB��
��QF=BF��
��QF=![]() QB��
QB��
��EF=EQ+QF=![]() PQ+
PQ+![]() QB=
QB=![]() PB��
PB��
��Rt��PBC��
��PC=4��BC=8��
��![]() ��
��
��EF=![]() PB=
PB=![]() ��
��
���M��N���˶������У��߶�EF�ij��Ȳ��䣬����Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ÿ��11�µ����һ���������Ǹж���,С�������˳����꼶����ͬѧ�ڸж��ڵ��콫�Ժ��ַ�ʽ�����л�������Լ����ˣ�������������Ϊ�������ࣺA�ੁ��������л��B�ੁ����绰��C�ੁ��������Ϣ���ţ�D�ੁ��д���ţ��������������Ƴ���ͼ������������ͳ��ͼ������ͳ��ͼ��

�������ͼ���ṩ����Ϣ������и��⣺
��1����ȫ����ͳ��ͼ��
��2����A���ͬѧ�У���3������ͬһ�༶��������1��ѧ�����֣�����������3������������λͬѧ���ָж���������Σ���������״ͼ����������������˶�û��ѧ�����ֵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC=��ACB��AD��BD��CD�ֱ�ƽ�֡�ABC����ǡ�EAC���ڽǡ�ABC����ǡ�ACF�����½��ۣ���AD��BC���ڡ�ACB=2��ADB���ۡ�ADC=90�㩁��ABD���ܡ�BDC=��BAC��������ȷ�Ľ����У� �� 
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����������ݳ������У�10λ��ί��ijλ���ֵĴ�ֱַ��ǣ�9.5��9.8��9.4��9.5��9.6��9.3��9.6��9.4��9.3��9.4�����������ݵ�������________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���涨�����š�&��Ϊѡ���������ϴ��������㣬����Ϊѡ�������н�С�������㣬��4��3������2&5���Ľ��Ϊ__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧ������MODE MODE 1��ʹ��ʾ����ʾD����sin90���ֵ�����°���˳����ȷ���ǣ�������
A.sin �� 9=
B.9��sin=
C.sin �� 9��0=
D.9��0=
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1�������ȱߡ�ABD����CBD�ı߳���Ϊ2������ABD��AC��������ƽ��k����λ����A��B��D���λ�ã��õ�ͼ2��������˵��������Ӱ���ֵ��ܳ�Ϊ4���ڵ�k=1ʱ��ͼ����Ӱ����Ϊ�������Σ�������Ӱ���ֺͿհײ��ֵ������ȣ���k=![]() �� ������ȷ��˵���ǣ�������
�� ������ȷ��˵���ǣ�������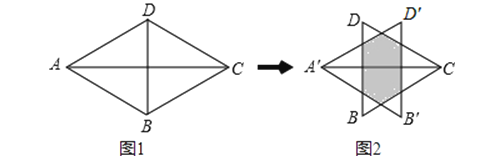
A.��
B.�٢�
C.�ڢ�
D.�٢ڢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com