
如图,AB∥CD,直线EF分别交AB,CD于M,N两点,将一个含有45°角的直角三角尺按如图所示的方式摆放,若∠EMB=75°,则∠PNM等于( )
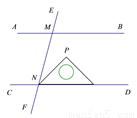
A. 15° B. 25° C. 30° D. 45°
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017届广东省业考试押题卷(一)数学试卷(解析版) 题型:解答题
某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.
(1)该班男生和女生各有多少人?
(2)某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?
查看答案和解析>>
科目:初中数学 来源:【全国百强校】2016-2017学年广东省中山纪念中学、广州市第六中学珠江中学七年级下学期期中考试数学试卷(解析版) 题型:单选题
把方程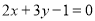 改写成含
改写成含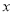 的式子表示
的式子表示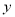 的形式为
的形式为
A. 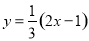 B.
B. 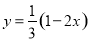 C.
C. 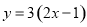 D.
D. 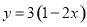
查看答案和解析>>
科目:初中数学 来源:2017届北京市东城区九年级5月综合练习(一模)数学试卷(解析版) 题型:单选题
图1是某娱乐节目中一个游戏环节的录制现场,场地由等边△ADE和正方形ABCD组成,正方形ABCD两条对角线交于点O,在AD的中点P处放置了一台主摄像机.游戏参与者行进的时间为x,与主摄像机的距离为y,若游戏参与者匀速行进,且表示y与x的函数关系式大致如图2所示,则游戏参与者的行进路线可能是( )
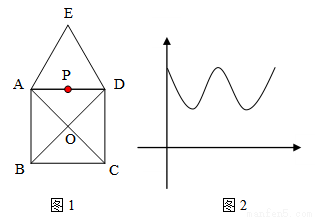
A. A→O→D B. E→A→C C. A→E→D D. E→A→B
查看答案和解析>>
科目:初中数学 来源:2017届北京市东城区九年级5月综合练习(一模)数学试卷(解析版) 题型:解答题
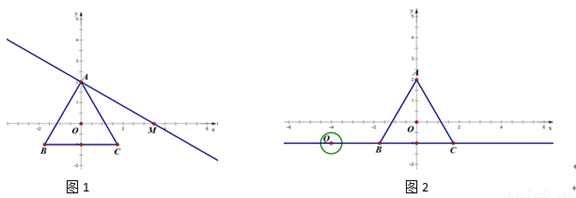
设平面内一点到等边三角形中心的距离为d,等边三角形的内切圆半径为r,外接圆半径为R .对于一个点与等边三角形,给出如下定义:满足r≤d≤R的点叫做等边三角形的中心关联点.在平面直角坐标系xOy中,等边△ABC的三个顶点的坐标分别为A(0,2),B(﹣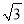 ,﹣1),C(
,﹣1),C(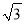 ,﹣1).
,﹣1).
(1)已知点D(2,2),E(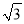 ,1),F(
,1),F(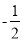 ,﹣1).在D,E,F中,是等边△ABC的中心关联点的是 ;
,﹣1).在D,E,F中,是等边△ABC的中心关联点的是 ;
(2)如图1,过点A作直线交x轴正半轴于M,使∠AMO=30°.
①若线段AM上存在等边△ABC的中心关联点P(m,n),求m的取值范围;
②将直线AM向下平移得到直线y=kx+b,当b满足什么条件时,直线y=kx+b上总存在等边△ABC的中心关联点;(直接写出答案,不需过程)
(3)如图2,点Q为直线y=﹣1上一动点,⊙Q的半径为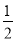 .当Q从点(﹣4,﹣1)出发,以每秒1个单位的速度向右移动,运动时间为t秒.是否存在某一时刻t,使得⊙Q上所有点都是等边△ABC的中心关联点?如果存在,请直接写出所有符合题意的t的值;如果不存在,请说明理由.
.当Q从点(﹣4,﹣1)出发,以每秒1个单位的速度向右移动,运动时间为t秒.是否存在某一时刻t,使得⊙Q上所有点都是等边△ABC的中心关联点?如果存在,请直接写出所有符合题意的t的值;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2017届北京市东城区九年级5月综合练习(一模)数学试卷(解析版) 题型:解答题
列方程或方程组解应用题:
在某场CBA比赛中,某位运动员的技术统计如下表所示:
技术 | 上场时间(分钟) | 出手投篮(次) | 投中 (次) | 罚球得分(分) | 篮板 (个) | 助攻(次) | 个人总得分(分) |
数据 | 38 | 27 | 11 | 6 | 3 | 4 | 33 |
注:(1)表中出手投篮次数和投中次数均不包括罚球;
(2)总得分=两分球得分+三分球得分+罚球得分.
根据以上信息,求本场比赛中该运动员投中两分球和三分球各几个.
查看答案和解析>>
科目:初中数学 来源:2017届北京市东城区九年级5月综合练习(一模)数学试卷(解析版) 题型:单选题
如图,AB∥CD,直线EF分别交AB,CD于M,N两点,将一个含有45°角的直角三角尺按如图所示的方式摆放,若∠EMB=75°,则∠PNM等于( )
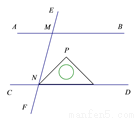
A. 15° B. 25° C. 30° D. 45°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com