Question

15．已知：如图，四边形ABCD是平行四边形，在边AB的延长线上截取BE=AB，点F在AE的延长线上，CE和DF交于点M，BC和DF交于点N．联结BD．
（1）求证：△BND∽△CNM；
（2）如果AD²=AB•AF，求证：CM•AB=DM•CN．

Answer 1

分析 （1）利用平行四边形的性质得AB=CD，AB∥CD，再证明四边形BECD为平行四边形得到BD∥CE，根据相似三角形的判定方法，由CM∥DB可判断△BND∽△CNM；
（2）先利用AD²=AB•AF可证明△ADB∽△AFD，则∠1=∠F，再根据平行线的性质得∠F=∠4，∠2=∠3，所以∠3=∠4，加上∠NMC=∠CMD，于是可判断△MNC∽△MCD，所以MC：MD=CN：CD，然后利用CD=AB和比例的性质即可得到结论．

解答 证明：（1）∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，
而BE=AB，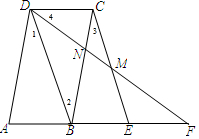
∴BE=CD，
而BE∥CD，
∴四边形BECD为平行四边形，
∴BD∥CE，
∵CM∥DB，
∴△BND∽△CNM；
（2）∵AD²=AB•AF，
∴AD：AB=AF：AD，
而∠DAB=∠FAD，
∴△ADB∽△AFD，
∴∠1=∠F，
∵CD∥AF，BD∥CE，
∴∠F=∠4，∠2=∠3，
∴∠3=∠4，
而∠NMC=∠CMD，
∴△MNC∽△MCD，
∴MC：MD=CN：CD，
∴MC•CD=MD•CN，
而CD=AB，
∴CM•AB=DM•CN．

点评 本题考查了三角形相似的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形．在运用相似三角形的性质时主要利用相似比计算线段的长．也考查了平行四边形的判定与性质．