Question

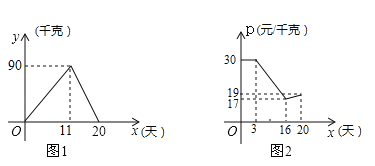
【题目】小明家今年种植的草莓喜获丰收，采摘上市20天全部销售完，爸爸让他对今年的销售情况进行跟踪记录，小明利用所学的数学知识将记录情况绘成图象（所得图象均为线段），日销售量y（单位：千克）与上市时间x（单位：天）的函数关系如图1所示，草莓的销售价p（单位：元/千克）与上市时间x（单位：天）的函数关系如图2所示设第x天的日销售额为w（单位：元）

（1）第11天的日销售额w为　 　元；

（2）观察图象，求当16≤x≤20时，日销售额w与上市时间x之间的函数关系式及w的最大值；

（3）若上市第15天时，爸爸把当天能销售的草莓批发给了邻居马叔叔，批发价为每千克15元，马叔叔到市场按照当日的销售价p元千克将批发来的草莓全部售完，他在销售的过程中，草莓总质量损耗了2%．那么，马叔叔支付完来回车费20元后，当天能赚到多少元？

Answer 1

【答案】（1）1980；（2）w＝﹣5（x﹣1）2+180， w有最大值是680元；（3）112元

【解析】

（1）当3≤x＜16时，设p与x的关系式为p＝kx＋b，当x＝11时，代入解析式求出p的值，由销售金额＝单价×数量就可以求出结论；

（2）根据两个图象求得两个一次函数解析式，进而根据销售问题的等量关系列出二次函数解析式即可；

（3）当x＝15时代入（2）的解析式求出p的值，再当x＝15时代入（1）的解析式求出y的值，再由利润＝销售总额进价总额车费就可以得出结论．

解：（1）当3≤x≤16时设p与x之间的函数关系式为p＝kx+b

依题意得把（3，30），（16，17）代入，

解得

∴p＝﹣x+33

当x＝11时，p＝22

所以90×22＝1980

答：第11天的日销售额w为1980元．

故答案为1980；

（2）当11≤x≤20时设y与x之间的函数关系式为y＝k1x+b1，

依题意得把（20，0），（11，90）代入得

解得

∴y＝﹣10x+200

当16≤x≤20时设p与x之间的函数关系式为：p＝k2x+b2

依题意得，把（16，17），（20，19）代入得

解得k2＝，b2＝9：

∴p＝x+9

w＝py＝（x+9）（﹣10x+200）

＝﹣5（x﹣1）2+1805

∴当16≤x≤20时，w随x的增大而减小

∴当x＝16时，w有最大值是680元．

（3）由（1）得当3≤x≤16时，p＝﹣x+33

当x＝15时，p＝﹣15+33＝18元，

y＝﹣10×15+200＝50千克

利润为：50（1﹣2%）×18﹣50×15﹣20＝112元

答：当天能赚到112元．