
 如图是一个长方体盒子(尺寸如图所示),在长方体下底部的A点有一只蚂蚁,它想吃到上底面B点的食物(BC=3cm),需爬行的最短路程是多少?
如图是一个长方体盒子(尺寸如图所示),在长方体下底部的A点有一只蚂蚁,它想吃到上底面B点的食物(BC=3cm),需爬行的最短路程是多少? 分析 先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.根据两点之间,线段最短,在平面图形上构造直角三角形解决问题.
解答 解:①将左面与上面展开在同一平面内,得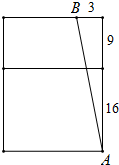
AB=$\sqrt{{3}^{2}+2{5}^{2}}$=$\sqrt{634}$;
②将正面与上面展开在同一平面内,得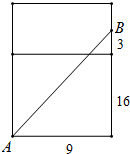
AB=$\sqrt{{9}^{2}+1{9}^{2}}$=$\sqrt{442}$;
③将正面与右面展开在同一平面内,得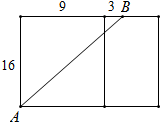
AB=$\sqrt{1{6}^{2}+1{2}^{2}}$=$\sqrt{400}$;
∵$\sqrt{400}$<$\sqrt{442}$<$\sqrt{634}$,
∴爬行的最短路程是$\sqrt{400}$=20cm.
点评 本题主要考查了平面展开-最短路径问题,解决问题的关键是将立体图形展开成平面图形,运用勾股定理进行计算.解题时注意分类思想的运用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)…,如果(1,0)是第一个点,探究规律如下:
如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)…,如果(1,0)是第一个点,探究规律如下:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
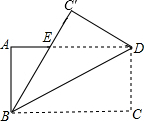 如图,矩形ABCD的长为8,宽为6,现将矩形沿对角线BD折叠,C点到达C′处,C′B交AD于E.
如图,矩形ABCD的长为8,宽为6,现将矩形沿对角线BD折叠,C点到达C′处,C′B交AD于E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com