
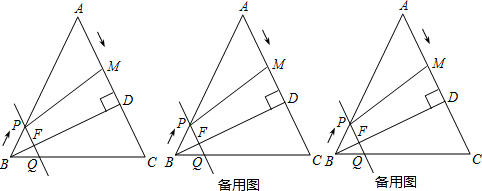
分析 (1)当四边形PQCM是平行四边形时,PM∥BC,得出AP=AM,列出方程,解方程即可;
(2)分类讨论:①若PQ=PM,作PO⊥AC于E,由平行线得出三角形相似,得出比例式,根据题意列出方程,解方程即可;
②若PQ=QM,作QN⊥AC于N,根据题意列出方程,解方程即可;
(3)当⊙E与BC相切时,切点为K,连接EK,则EK⊥BC;作PG⊥BC于G,AS⊥BC于S,MH⊥BC于H,根据梯形的中位线得出EK=$\frac{1}{2}$(PG+MH),PM=2EK,根据勾股定理列出方程,解方程即可.
解答 解:(1)当四边形PQCM是平行四边形时,PM∥BC,
则△APM∽△ABC,BP=t,AM=2t,AP=10-2t,
∵AB=AC=10cm,
∴AP=AM,
∴10-t=2t,
解得:t=$\frac{10}{3}$;
即当四边形PQCM是平行四边形时,t=$\frac{10}{3}$;
(2)∵PQ∥AC,AB=AC,
∴BP=PQ=t;分类讨论:
①若PQ=PM,作PO⊥AC于E,如图1所示: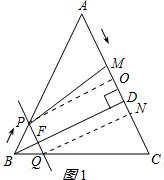 ∵PQ∥AC,
∵PQ∥AC,
∴△BPQ∽△BCA,
∴则$\frac{BF}{BD}=\frac{PQ}{AC}$,即$\frac{BF}{8}=\frac{t}{10}$,
∴BF=$\frac{4}{5}$t,
∴DF=8-$\frac{4}{5}$t,
又∵PO⊥AC,BD⊥AC,
∴PO∥BD,AD=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∴$\frac{AO}{AD}=\frac{PO}{BD}$,CD=4,
∴AO=6-$\frac{3}{5}$t,
∴OM=6-$\frac{3}{5}$t-2t=6-$\frac{13}{5}$t,
∵PM2=PO2+OM2,∴${(8-\frac{4}{5}t)^2}+{(6-\frac{13}{5}t)^2}={t^2}$,
整理得:8t2-55t+125=0,
∵b2-4ac<0,
∴此方程无解;
②若PQ=QM,作QN⊥AC于N,如图1所示:
则QN∥BD,∴△CNQ∽CDB,
∴$\frac{CN}{CD}=\frac{QN}{BD}$,
∴CN=4-$\frac{2}{5}$t,
∴MN=10-2t-(4-$\frac{2}{5}$t)=6-$\frac{8}{5}$t,
∵QM2=QN2+MN2,
∴${(6-\frac{8}{5}t)^2}+{(8-\frac{4}{5}t)^2}={t^2}$,
解得t=10(舍),t=$\frac{50}{11}$;
③若PM=QM,则M是ON的中点,
∴OM=MN,
∴6-$\frac{8}{5}$t=$\frac{13}{5}$t-6,
解得:t=$\frac{20}{7}$;
∴当t=$\frac{50}{11}$或$\frac{20}{7}$时,△PQM是等腰三角形;
(3)假设存在;
当⊙E与BC相切时,切点为K,连接EK,则EK⊥BC;
作PG⊥BC于G,AS⊥BC于S,MH⊥BC于H,则EK∥PG∥AS∥MH,如图2所示: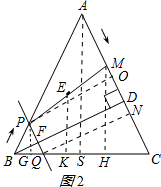
∵BC=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$,
∴BS=2$\sqrt{5}$,
∴AS=$\sqrt{1{0}^{2}-(2\sqrt{5)^{2}}}$=4$\sqrt{5}$,
∴$\frac{PG}{BP}=\frac{AS}{AB}$=$\frac{4\sqrt{5}}{10}=\frac{2\sqrt{5}}{5}$,
∴PG=$\frac{2\sqrt{5}}{5}$t,
同理:MH=$\frac{2\sqrt{5}}{5}$(10-2t),
∵E为PM的中点,
∴K为GH的中点,
∴EK为梯形PGHM的中位线,
∴EK=$\frac{1}{2}$(PG+MH)=$\frac{\sqrt{5}}{5}$(10-t),
∵PM=2EK,
∴${(8-\frac{4}{5}t)^2}+{(6-\frac{13}{5}t)^2}={[{\frac{2}{{\sqrt{5}}}(10-t)}]^2}$
解得t=$\frac{10}{3}$,t=$\frac{10}{11}$;
∴当t=$\frac{10}{3}$或$\frac{10}{11}$时,⊙E与BC相切.
点评 本题是圆的综合题,考查了相似三角形的判定与性质、勾股定理、一元二次方程的解法、梯形中位线定理等知识;本题难度较大,综合性强;特别是(2)(3)中,通过三角形相似得出比例式,再由勾股定理列出方程;根据题意列出方程是解决问题的关键.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
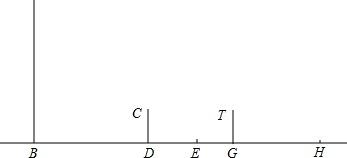
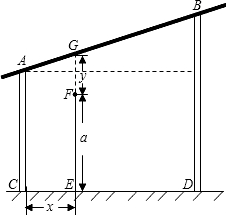 有一个测量弹跳力的体育器材,如图所示,竖杆AC、BD的长度分别为200厘米、300厘米,CD=300厘米.现有一人站在斜杆AB下方的点E处,直立、单手上举时中指指尖(点F)到地面的高度为EF,屈膝尽力跳起时,中指指尖刚好触到斜杆AB上的点G处,此时,就将EG与EF的差值y(厘米)作为此人此次的弹跳成绩.
有一个测量弹跳力的体育器材,如图所示,竖杆AC、BD的长度分别为200厘米、300厘米,CD=300厘米.现有一人站在斜杆AB下方的点E处,直立、单手上举时中指指尖(点F)到地面的高度为EF,屈膝尽力跳起时,中指指尖刚好触到斜杆AB上的点G处,此时,就将EG与EF的差值y(厘米)作为此人此次的弹跳成绩.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com