
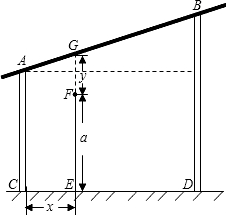
 有一个测量弹跳力的体育器材,如图所示,竖杆AC、BD的长度分别为200厘米、300厘米,CD=300厘米.现有一人站在斜杆AB下方的点E处,直立、单手上举时中指指尖(点F)到地面的高度为EF,屈膝尽力跳起时,中指指尖刚好触到斜杆AB上的点G处,此时,就将EG与EF的差值y(厘米)作为此人此次的弹跳成绩.
有一个测量弹跳力的体育器材,如图所示,竖杆AC、BD的长度分别为200厘米、300厘米,CD=300厘米.现有一人站在斜杆AB下方的点E处,直立、单手上举时中指指尖(点F)到地面的高度为EF,屈膝尽力跳起时,中指指尖刚好触到斜杆AB上的点G处,此时,就将EG与EF的差值y(厘米)作为此人此次的弹跳成绩.分析 (1)利用相似三角形的判定与性质得出△ANG∽△AMB,进而得出$\frac{AN}{AM}$=$\frac{CN}{BM}$,即可得出答案;
(2)当x=150cm,a=205cm时,直接代入(1)中所求得出即可.
解答 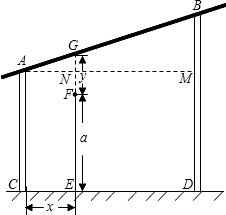 解:(1)过A作AM⊥BD于点M,交GE于N.
解:(1)过A作AM⊥BD于点M,交GE于N.
∵AC⊥CD,GE⊥CD,
∴四边形ACEN为矩形,
∴NE=AC,
又∵AC=200,EF=a,FG=y,
∴GN=GE-NE=a+y-200,
∵DM=AC=200,
∴BM=BD-DM=300-200=100,
又∵GN∥BD,
∴△ANG∽△AMB,
∴$\frac{AN}{AM}$=$\frac{CN}{BM}$,
即$\frac{x}{300}$=$\frac{a+y-200}{100}$,
∴y=$\frac{1}{3}$x-a+200;
(2)当x=150cm,a=205cm时,
y=1×150-205+200=45(cm),
y=45>40.
故该生弹跳成绩处于良好水平.
点评 此题主要考查了相似三角形的判定与性质,得出△ANG∽△AMB是解题关键.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:初中数学 来源: 题型:解答题
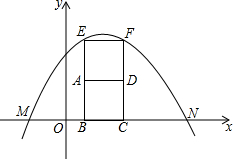 如图,抛物线y=ax2+bx+$\frac{3}{4}$经过M(-$\frac{1}{2}$,0),N($\frac{3}{2}$,0),正方形EADF、ABCD的边长均为m,边BC落在x轴上,点E、F在抛物线y=ax2+bx+$\frac{3}{4}$上.
如图,抛物线y=ax2+bx+$\frac{3}{4}$经过M(-$\frac{1}{2}$,0),N($\frac{3}{2}$,0),正方形EADF、ABCD的边长均为m,边BC落在x轴上,点E、F在抛物线y=ax2+bx+$\frac{3}{4}$上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9 | B. | 16 | C. | 22 | D. | 25 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com