练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．解不等式：$\frac{x+1}{4}$-$\frac{1}{6}$＜$\frac{2x-5}{3}$+$\frac{1}{2}$．

    分析 根据不等式的解法求解不等式．

    解答 解：去分母得：3x+3-2＜8x-20+6，
    移项合并同类项得：5x＞15，
    系数化为1得：x＞3．

    点评 本题考查了解简单不等式的能力，解不等式要依据不等式的基本性质：
    （1）不等式的两边同时加上或减去同一个数或整式不等号的方向不变；
    （2）不等式的两边同时乘以或除以同一个正数不等号的方向不变；
    （3）不等式的两边同时乘以或除以同一个负数不等号的方向改变．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    2．把二次函数y=x2向左平移1个单位，再向下平移2个单位，则平移后二次函数的解析式为y=（x+1）2-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．要使（x2+ax+1）（x4-6x3）的展开式中不含x4项，则a应等于$\frac{1}{6}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图，为了测量河的宽度AB，测量人员在高21m的建筑物CD的顶端D处测得河岸B处的俯角为45°，测得河对岸A处的俯角为30°（A、B、C在同一条直线上），则河的宽度AB约是多少m？（精确到0.1m）．（参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

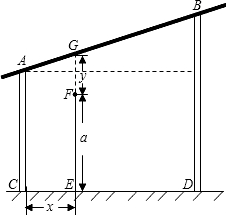    7．有一个测量弹跳力的体育器材，如图所示，竖杆AC、BD的长度分别为200厘米、300厘米，CD=300厘米．现有一人站在斜杆AB下方的点E处，直立、单手上举时中指指尖（点F）到地面的高度为EF，屈膝尽力跳起时，中指指尖刚好触到斜杆AB上的点G处，此时，就将EG与EF的差值y（厘米）作为此人此次的弹跳成绩．
    （1）设CE=x（厘米），EF=a（厘米），求出由x和a表示y的计算公式；
    （2）现有一男生，站在某一位置尽力跳起时，刚好触到斜杆．已知该同学弹跳时站的位置为x=150厘米，且a=205厘米．若规定y≥50，弹跳成绩为优；40≤y＜50时，弹跳成绩为良；30≤y＜40时，弹跳成绩为及格，那么该生弹跳成绩处于什么水平？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．已知y=y1+y2，y1与x成正比例，y2与x2成反比例，且当x=2时，y=0，当x=-1时，y=$\frac{9}{2}$，求y与x之间的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．观察如图的图形，找规律，填表答题．

    小梯形个数n　12　3　4…　n
    　图形的边数a　471013…3n+1
    （1）把表补充完整，并回答其中哪个是自变量，哪个是因变量？
    （2）图形的边数a是小梯形个数n的函数吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．计算：
    （1）-34+（-8）-5-（-23）；
    （2）-$\sqrt{16}$×（-$\frac{1}{2}$）2÷$\frac{1}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．解方程：
    （1）4x-3（20-x）+4=0；                      
    （2）$\frac{2x+1}{3}$-$\frac{x-1}{6}$=2；
    （3）$\frac{3x+1}{2}$-$\frac{7+x}{6}$=0；                  
    （4）$\frac{3+0.2x}{0.2}$-$\frac{0.2+0.03x}{0.01}$=0.75．

    查看答案和解析>>

    同步练习册答案