
 如图,为了测量河的宽度AB,测量人员在高21m的建筑物CD的顶端D处测得河岸B处的俯角为45°,测得河对岸A处的俯角为30°(A、B、C在同一条直线上),则河的宽度AB约是多少m?(精确到0.1m).(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,为了测量河的宽度AB,测量人员在高21m的建筑物CD的顶端D处测得河岸B处的俯角为45°,测得河对岸A处的俯角为30°(A、B、C在同一条直线上),则河的宽度AB约是多少m?(精确到0.1m).(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73) 分析 在Rt△ACD中,根据已知条件求出AC的值,再在Rt△BCD中,根据∠EDB=45°,求出BC=CD=21m,最后根据AB=AC-BC,代值计算即可.
解答 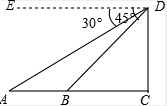 解:∵在Rt△ACD中,CD=21m,∠DAC=30°,
解:∵在Rt△ACD中,CD=21m,∠DAC=30°,
∴AC=$\frac{CD}{tan30°}$=$\frac{21}{\frac{\sqrt{3}}{3}}$=21$\sqrt{3}$m,
在Rt△BCD中,
∵∠EDB=45°,
∴∠DBC=45°,
∴BC=CD=21m,
∴AB=AC-BC=21$\sqrt{3}$-21≈15.3(m);
则河的宽度AB约是15.3m.
点评 此题考查了解直角三角形的应用,用到的知识点是俯角、特殊角的三角函数值等知识点,关键是要求学生能借助俯角构造直角三角形并解直角三角形.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
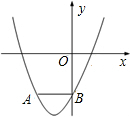 如图,已知二次函数y=x2+bx+c(c≠0)的图象经过点A(-2,m)(m<0),与y轴交于点B,AB∥x轴,且AB=OB.
如图,已知二次函数y=x2+bx+c(c≠0)的图象经过点A(-2,m)(m<0),与y轴交于点B,AB∥x轴,且AB=OB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
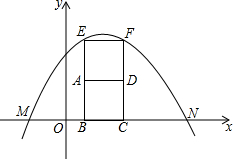 如图,抛物线y=ax2+bx+$\frac{3}{4}$经过M(-$\frac{1}{2}$,0),N($\frac{3}{2}$,0),正方形EADF、ABCD的边长均为m,边BC落在x轴上,点E、F在抛物线y=ax2+bx+$\frac{3}{4}$上.
如图,抛物线y=ax2+bx+$\frac{3}{4}$经过M(-$\frac{1}{2}$,0),N($\frac{3}{2}$,0),正方形EADF、ABCD的边长均为m,边BC落在x轴上,点E、F在抛物线y=ax2+bx+$\frac{3}{4}$上.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
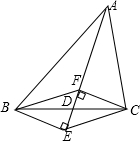 如图,AD是△ABC的中线,CF、BE分别垂直于AD,垂足分别为F、E,则四边形BECF是平行四边形,理由是一组对边平行且相等的四边形是平行四边形.
如图,AD是△ABC的中线,CF、BE分别垂直于AD,垂足分别为F、E,则四边形BECF是平行四边形,理由是一组对边平行且相等的四边形是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com