
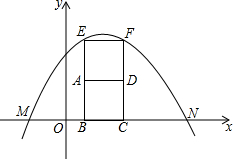
 如图,抛物线y=ax2+bx+$\frac{3}{4}$经过M(-$\frac{1}{2}$,0),N($\frac{3}{2}$,0),正方形EADF、ABCD的边长均为m,边BC落在x轴上,点E、F在抛物线y=ax2+bx+$\frac{3}{4}$上.
如图,抛物线y=ax2+bx+$\frac{3}{4}$经过M(-$\frac{1}{2}$,0),N($\frac{3}{2}$,0),正方形EADF、ABCD的边长均为m,边BC落在x轴上,点E、F在抛物线y=ax2+bx+$\frac{3}{4}$上.分析 (1)根据抛物线y=ax2+bx+$\frac{3}{4}$经过M(-$\frac{1}{2}$,0),N($\frac{3}{2}$,0),根据待定系数法求出a和b的值即可;
(2)把抛物线的一般表达式写出顶点坐标式,据此写出抛物线的对称轴;
(3)设点B的坐标为(n,0),则C点坐标为(n+m,0),根据正方形的知识求出E和F点的坐标,进而得到m和n的二元二次方程组,解方程求出m的值即可.
解答 解:(1)∵抛物线y=ax2+bx+$\frac{3}{4}$经过M(-$\frac{1}{2}$,0),N($\frac{3}{2}$,0),
∴$\left\{\begin{array}{l}{0=\frac{1}{4}a-\frac{1}{2}b+\frac{3}{4}}\\{0=\frac{9}{4}a+\frac{3}{2}b+\frac{3}{4}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=1}\end{array}\right.$.
∴抛物线的解析式为y=-x2+x+$\frac{3}{4}$;
(2)∵y=-x2+x+$\frac{3}{4}$;
∴y=-(x-$\frac{1}{2}$)2+1,
∴抛物线的对称轴为直线x=$\frac{1}{2}$;
(3)设点B的坐标为(n,0),则C点坐标为(n+m,0),
∵正方形EADF、ABCD的边长均为m,
∴E点坐标为(n,2m),F点坐标为(n+m,2m),
∵点E、F在抛物线y=-x2+x+$\frac{3}{4}$上,
∴$\left\{\begin{array}{l}{2m=-{n}^{2}+n+\frac{3}{4}}\\{2m=-(n+m)^{2}+m+n+\frac{3}{4}}\end{array}\right.$,
解得2n+m-1=0,
把n=$\frac{1-m}{2}$代入2m=-n2+n+$\frac{3}{4}$,
即2m=-$\frac{(1-m)^{2}}{4}+\frac{1-m}{2}+\frac{3}{4}$,
整理得m2-8m+4=0,
解得m=4±2$\sqrt{3}$,
由于|MN|=$\frac{3}{2}-(-\frac{1}{2})$=2,则m=4+2$\sqrt{3}$不符合题意,舍去,
则m的值为4-2$\sqrt{3}$.
点评 本题主要考查了二次函数的综合题的知识,此题涉及知识点较多,有待定系数法求二次函数的解析式,正方形的性质以及二次函数的性质,解答此题关键是求出抛物线的解析式,解答第(3)问时利用正方形的性质求出E和F点坐标,此题有一定的难度.


科目:初中数学 来源: 题型:选择题
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\sqrt{5}$ | B. | $\sqrt{5}$ | C. | ±$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,为了测量河的宽度AB,测量人员在高21m的建筑物CD的顶端D处测得河岸B处的俯角为45°,测得河对岸A处的俯角为30°(A、B、C在同一条直线上),则河的宽度AB约是多少m?(精确到0.1m).(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,为了测量河的宽度AB,测量人员在高21m的建筑物CD的顶端D处测得河岸B处的俯角为45°,测得河对岸A处的俯角为30°(A、B、C在同一条直线上),则河的宽度AB约是多少m?(精确到0.1m).(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
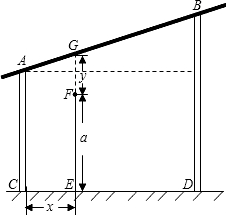 有一个测量弹跳力的体育器材,如图所示,竖杆AC、BD的长度分别为200厘米、300厘米,CD=300厘米.现有一人站在斜杆AB下方的点E处,直立、单手上举时中指指尖(点F)到地面的高度为EF,屈膝尽力跳起时,中指指尖刚好触到斜杆AB上的点G处,此时,就将EG与EF的差值y(厘米)作为此人此次的弹跳成绩.
有一个测量弹跳力的体育器材,如图所示,竖杆AC、BD的长度分别为200厘米、300厘米,CD=300厘米.现有一人站在斜杆AB下方的点E处,直立、单手上举时中指指尖(点F)到地面的高度为EF,屈膝尽力跳起时,中指指尖刚好触到斜杆AB上的点G处,此时,就将EG与EF的差值y(厘米)作为此人此次的弹跳成绩.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 小梯形个数n | 1 | 2 | 3 | 4 | … | n |
| 图形的边数a | 4 | 7 | 10 | 13 | … | 3n+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com