练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．观察如图的图形，找规律，填表答题．

    小梯形个数n　12　3　4…　n
    　图形的边数a　471013…3n+1
    （1）把表补充完整，并回答其中哪个是自变量，哪个是因变量？
    （2）图形的边数a是小梯形个数n的函数吗？

    分析 （1）根据图形的变化，可得自变量，因变量；
    （2）根据函数的定义，可得答案．

    解答 解：（1）图形的变数随着梯形个数的变化而变化，梯形的个数是自变量，图形的边数是因变量；
    （2）图形的边数a是小梯形个数n的函数，理由是有一个n就有唯一确定的a值与之对应，a是n的函数．

    点评 本题考查了函数的概念，利用了函数的定义，观察图形发现规律是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．小李家用40m长的篱笆围成一个一边靠墙（墙足够长）的矩形菜园，如图．
    （1）写出这块菜园的面积y（m2）与垂直于墙的边长x（m）之间的函数解析式；
    （2）直接写出x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

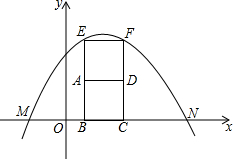    15．如图，抛物线y=ax2+bx+$\frac{3}{4}$经过M（-$\frac{1}{2}$，0），N（$\frac{3}{2}$，0），正方形EADF、ABCD的边长均为m，边BC落在x轴上，点E、F在抛物线y=ax2+bx+$\frac{3}{4}$上．
    （1）求此抛物线所对应的函数关系式；
    （2）求此抛物线的对称轴；
    （3）求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．解不等式：$\frac{x+1}{4}$-$\frac{1}{6}$＜$\frac{2x-5}{3}$+$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．当x=-1$\frac{1}{5}$时，求（1+$\frac{2}{x-1}$）3（1-$\frac{3}{x-2}$）2÷（$\frac{{x}^{2}-4x-5}{{x}^{2}-3x+2}$）2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

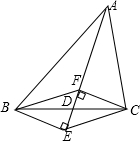    9．如图，AD是△ABC的中线，CF、BE分别垂直于AD，垂足分别为F、E，则四边形BECF是平行四边形，理由是一组对边平行且相等的四边形是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．某检修小组乘汽车沿公路检修线路，约定前进为正，后退为负，某天自P地出发到收工时所走路线（单位：千米）为：+11，-4，-3，+5，-6，+16，-4，-10，-6．问收工时距P地多远？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

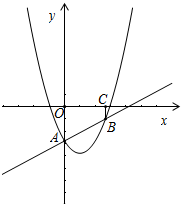    2．如图，抛物线y=x2+bx+c与y轴交于点A（0，$-\frac{25}{9}$），与过点A的直线交于点B（$\frac{8}{3}$，-1），过点B作BC⊥x轴，垂足为C．
    （1）求抛物线和直线的解析式；
    （2）点P是x轴正半轴上的一动点，过点P作PN⊥x轴，交直线AB于点M，交抛物线于点N，设OP的长度为n．
    ①当点P在线段OC上（不与点O、C重合）时，试用含n的代数式表示线段PM的长度；
    ②连接CM、BN，探究是否存在点P，使以B、C、M、N为顶点的四边形为平行四边形？若存在，求此时点P坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

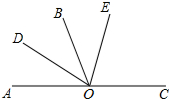    3．如图，已知O是直线AC上一点，OB是一条射线，OD平分∠AOB，OE在∠BOC内，2∠BOE=∠EOC，∠DOE=70°，求∠EOC的度数．

    查看答案和解析>>

    同步练习册答案