
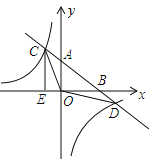
【题目】如图,一次函数y=ax+b的图象与反比例函数![]() 的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO=
的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)求一次函数的解析式和反比例函数的解析式;
(2)求△OCD的面积;
(3)根据图象直接写出一次函数的值大于反比例函数的值时,自变量x的取值范围.
【答案】(1)![]() ,
, ![]() ;(2)8;(3)x<﹣2或0<x<6.
;(2)8;(3)x<﹣2或0<x<6.
【解析】试题分析:(1)根据已知条件求出A、B、C点坐标,用待定系数法求出直线AB和反比例函数的解析式;
(2)联立一次函数的解析式和反比例的函数解析式可得交点D的坐标,从而根据三角形面积公式求解;
(3)根据函数的图象和交点坐标即可求解.
试题解析:解:(1)∵OB=4,OE=2,∴BE=2+4=6.
∵CE⊥x轴于点E,tan∠ABO=![]() =
=![]() ,∴OA=2,CE=3,∴点A的坐标为(0,2)、点B的坐标为C(4,0)、点C的坐标为(﹣2,3).
,∴OA=2,CE=3,∴点A的坐标为(0,2)、点B的坐标为C(4,0)、点C的坐标为(﹣2,3).
∵一次函数y=ax+b的图象与x,y轴交于B,A两点,∴![]() ,解得:
,解得: 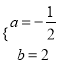 .
.
故直线AB的解析式为![]() .
.
∵反比例函数![]() 的图象过C,∴3=
的图象过C,∴3=![]() ,∴k=﹣6,∴该反比例函数的解析式为
,∴k=﹣6,∴该反比例函数的解析式为![]() ;
;
(2)联立反比例函数的解析式和直线AB的解析式可得: 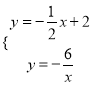 ,可得交点D的坐标为(6,﹣1),则△BOD的面积=4×1÷2=2,△BOC的面积=4×3÷2=6,故△OCD的面积为2+6=8;
,可得交点D的坐标为(6,﹣1),则△BOD的面积=4×1÷2=2,△BOC的面积=4×3÷2=6,故△OCD的面积为2+6=8;
(3)由图象得,一次函数的值大于反比例函数的值时x的取值范围:x<﹣2或0<x<6.


科目:初中数学 来源: 题型:
【题目】“中国制造”是世界上认知度最高的标签之一,因此,我县越来越多的群众选择购买国产空调,已知购买1台A型号的空调比1台B型号的空调少200元,购买2台A型号的空调与3台B型号的空调共需11200元,求A、B两种型号的空调的购买价各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
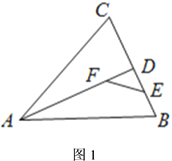
【题目】有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.
(1)如图1,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点.求证:四边形
上的点.求证:四边形![]() 是邻余四边形;
是邻余四边形;
(2)如图2,已知![]() ,点
,点![]() 在
在![]() 的垂直平分线上,
的垂直平分线上,![]() 在边
在边![]() 上,
上,![]() 是
是![]() 内一点, 连接
内一点, 连接![]() ,
,![]() ,
,![]() ,
,![]() ,若四边形
,若四边形![]() 是邻余四边形,
是邻余四边形,![]() 是邻余线.
是邻余线.
①![]() 与
与![]() 有什么位置关系?说明理由.
有什么位置关系?说明理由.
②判断![]() 形状,说明理由.
形状,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某市实施城中村改造的过程中,“旺鑫”拆迁工程队承包了一项10000 m2的拆迁工程.由于准备工作充分,实际拆迁效率比原计划提高了25%,提前2天完成了任务,请解答下列问题:
(1)求“旺鑫”拆迁工程队现在平均每天拆迁多少平方米;
(2)为了尽量减少拆迁给市民带来的不便,在拆迁工作进行了2天后,“旺鑫”拆迁工程队的领导决定加快拆迁工作,将余下的拆迁任务在5天内完成,那么“旺鑫”拆迁工程队平均每天至少再多拆迁多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣2,0),B(3,0).
(1)在y轴上找一点C,使之满足△ABC的面积为12,求点C的坐标.
(2)在y轴上找一点D,使BD=AB,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )

A. 20° B. 25° C. 30° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他费用80元.

(1)请直接写出y与x之间的函数关系式;
(2)如果每天获得160元的利润,销售单价为多少元?
(3)设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com