
【题目】如图,四边形![]() 内接于
内接于![]() ,
,![]() 为直径,
为直径,![]() 平分
平分![]() ,
,![]() 与
与![]() 相交于
相交于![]() .
.

![]() 求证:
求证:![]() ;
;
![]() 若直径
若直径![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)证△CBE∽△DBC,得出比例式,即可得出答案;
(2)求出△ACB是等腰直角三角形,求出BC,根据(1)和已知求出BE、DE,根据相交弦定理求出即可.
(1)∵BD平分∠ADC,∴∠ADB=∠CDB.
∵∠ADB=∠ECB,∴∠BDC=∠BCE.
∵∠DBC=∠CBE,∴△CBE∽△DBC,∴![]() =
=![]() ,∴BC2=BEBD.
,∴BC2=BEBD.
(2)∵∠ADB=∠CDB,∠ADB=∠ACB,∠CDB=∠CAB,∴∠ACB=∠BAC,∴AB=BC.
∵AC为直径,∴∠ABC=90°,∴△ABC为等腰直角三角形.在Rt△ABC中,∠ABC=90°,AB=BC,AC=6![]() ,由勾股定理得:BC=6.
,由勾股定理得:BC=6.
∵BC2=BEBD,BE:ED=3:1,∴设ED=x,则BE=3x,BD=4x,∴36=12x2,解得:x=![]() ,设OE=y,则AE=3
,设OE=y,则AE=3![]() +y,CE=3
+y,CE=3![]() ﹣y.
﹣y.
由相交弦定理得:(3![]() +y)(3
+y)(3![]() ﹣y)=3
﹣y)=3![]()
![]() ,解得:y=3,即OE=3.
,解得:y=3,即OE=3.


科目:初中数学 来源: 题型:
【题目】甲、乙两名学生的十次数学竞赛训练成绩的平均分分别是![]() 和
和![]() ,成绩的方差分别是
,成绩的方差分别是![]() 和
和![]() ,现在要从两人中选择发挥稳定的一人参加数学竞赛,下列说法正确的是( )
,现在要从两人中选择发挥稳定的一人参加数学竞赛,下列说法正确的是( )
A. 甲、乙两人平均分相当,选谁都可以
B. 乙的平均分比甲高,选乙
C. 乙的平均分和方差都比甲高,成绩比甲稳定,选乙
D. 两人的平均分相当,甲的方差小,成绩比乙稳定,选甲
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种产品的原料提价,因而厂家决定对产品提价,现有三种方案:
方案(一):第一次提价![]() ,第二次提价
,第二次提价![]() ;
;
方案(二):第一次提价![]() ,第二次提价
,第二次提价![]() ;
;
方案(三):第一、二次提价均为![]() ;
;
其中![]() ,
,![]() 是不相等的正数.
是不相等的正数.
有以下说法:
①方案(一)、方案(二)提价一样;
②方案(一)的提价也有可能高于方案(二)的提价;
③三种方案中,以方案(三)的提价最多;
④方案(三)的提价也有可能会低于方案(一)或方案(二)的提价.
其中正确的有( )
A.②③B.①③C.①④D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABP与![]() 是两个全等的等边三角形,且
是两个全等的等边三角形,且![]() ,有下列四个结论:①
,有下列四个结论:①![]() ,②
,②![]() ,③
,③![]() ,④四边形ABCD是轴对称图形,其中正确的有
,④四边形ABCD是轴对称图形,其中正确的有
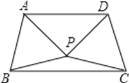
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【发现证明】
如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.
【类比引申】
(1)如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;
【联想拓展】
(2)如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
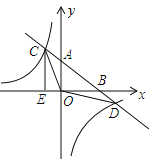
【题目】如图,一次函数y=ax+b的图象与反比例函数![]() 的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO=
的图象交于C,D两点,与x,y轴交于B,A两点,且tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)求一次函数的解析式和反比例函数的解析式;
(2)求△OCD的面积;
(3)根据图象直接写出一次函数的值大于反比例函数的值时,自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com