
【题目】定义:在一个三角形中,若存在两条边x和y,使得y=x2,则称此三角形为“平方三角形”,x称为平方边.
(1)“若等边三角形为平方三角形,则面积为![]() 是 命题;“有一个角为30°且有一条直角边为2的直角三角形是平方三角形”是 命题;(填“真”或“假”)
是 命题;“有一个角为30°且有一条直角边为2的直角三角形是平方三角形”是 命题;(填“真”或“假”)
(2)若a,b,c是平方三角形的三条边,平方边a=2,若三角形中存在一个角为60°,求c的值;
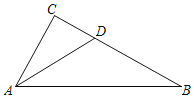
(3)如图,在△ABC中,D是BC上一点.
①若∠CAD=∠B,CD=1,求证,△ABC是平方三角形;
②若∠C=90°,BD=1,AC=m,CD=n,求tan∠DAB.(用含m,n的代数式表示)
【答案】(1)真,假;(2)c的长为4或1+![]() ;(3)①见解析;②tan∠DAB=
;(3)①见解析;②tan∠DAB=![]()
【解析】
(1)①根据平方三角形的定义,求出等边三角形的边长即可判断.②分两种情形分别判断即可.
(2)为a,b,c是平方三角形的三条边,平方边a=2,三角形中存在一个角为60°,只有∠B或∠C=60°,∠A不可能为60°,不妨设∠B=60°,BC=2,分两种情形:如图1中,①当c=a2时.②如图2中,当b=a2=4时,作CH⊥AB于H.求出AB即可.
(3)①证明△CAD∽△CBA,利用相似三角形的性质即可解决问题.
②如图4中,作DH⊥AB于H.利用相似三角形的性质求出DH,AH即可解决问题.
解:(1)∵等边三角形为平方三角形,
∴根据平方三角形的定义可知:等边三角形的边长为1,
∴等边三角形的面积=![]() ,
,
∴①是真命题.
当直角三角形中,30°所对的直角边为2时,斜边为4,满足平方三角形的定义,
当直角三角形中,和30°相邻的直角边是2时,不是平方三角形,
故②是假命题,
故答案为真,假.
(2)因为a,b,c是平方三角形的三条边,平方边a=2,三角形中存在一个角为60°,
只有∠B或∠C=60°,∠A不可能为60°,不妨设∠B=60°,BC=2,
如图1中,①当c=a2时,∵a=2,
∴c=22=4.
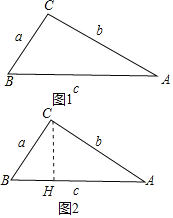
如图2中,当b=a2=4时,作CH⊥AB于H.
在Rt△BCH中,∵∠B=60°,∠CHB=90°,BC=2,
∴BH=![]() BC=1,CH=
BC=1,CH=![]() BH=
BH=![]() ,
,
在Rt△ACH中,AH=![]() =
=![]() ,
,
∴c=AB=BH+AH=1+![]() ,
,
综上所述,c的长为4或1+![]() .
.
(3)①如图3中,
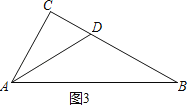
∵∠C=∠C,∠CAD=∠B,
∴△CAD∽△CBA,
∴![]() =
=![]() ,
,
∴AC2=CDCB,
∵CD=1,
∴AC2=BC,
∴△ABC是平方三角形.
②如图4中,作DH⊥AB于H.
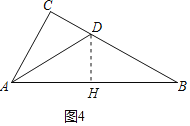
在Rt△ABC中,∵∠C=90°,AC=m,BC=CD+BD=1+n,
∴AB=![]() ,
,
∵DH⊥AB,
∴∠DHB=90°,
∵∠B=∠B,∠DHB=∠C=90°,
∴△BHD∽△BCA,
∴![]() ,
,
∴ ,
,
∴DH=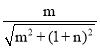 ,BH=
,BH=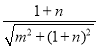 ,
,
∴AH=![]() ﹣
﹣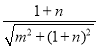 ,
,
∴tan∠DAB=![]() =
=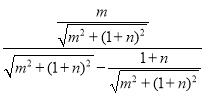 =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,过点B的直线与对角线AC、边AD分别交于点E和F.过点E作EG∥BC,交AB于G,则图中相似三角形有( )
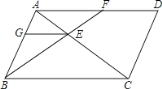
A. 7对 B. 6对 C. 5对 D. 4对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在平面直角坐标系中,网格中每个小正方形的边长均为1,三个顶点的坐标分别为A(0,2),B(4,0),C(4,6).
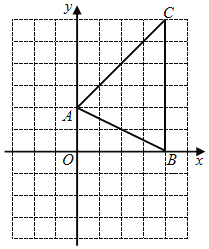
(1)画出△ABC向左平移2个单位长度得到的△A1B1C1,并写出点B1的坐标;
(2)以点O为位似中心,在第三象限画出△A2B2C2,使△A2B2C2与△ABC位似,且相似比为1:2,直接写出点C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里有1个红球,1个黄球和n个白球,它们除颜色外其余都相同.
(1)从这个袋子里摸出一个球,记录其颜色,然后放回,摇均匀后,重复该实验,经过大量实验后,发现摸到白球的频率稳定于0.5左右,求n的值;
(2)在(1)的条件下,先从这个袋中摸出一个球,记录其颜色,放回,摇均匀后,再从袋中摸出一个球,记录其颜色.请用画树状图或者列表的方法,求出先后两次摸出不同颜色的两个球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将四边形ABCD绕原点O旋转180°得四边形A′B′C′D′.
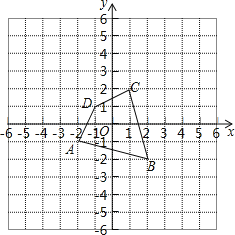
(1)画出旋转后的四边形A′B′C′D′;
(2)写出A′、B′、C′、D′的坐标;
(3)若每个小正方形的边长是1,请直接写出四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图一次函数y=kx+b的图象与反比例函数![]() (x > 0)的图象交于A(2,–l),B(
(x > 0)的图象交于A(2,–l),B(![]() ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C.
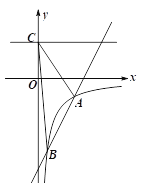
(1)求反比例函数的解析式;
(2)求一次函数的解析式;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店销售一批衬衫,每件进价![]() 元,开始以每件
元,开始以每件![]() 元的价格销售,每星期能卖出
元的价格销售,每星期能卖出![]() 件,后来因库存积压,决定降价销售,经两次降价后的每件售价
件,后来因库存积压,决定降价销售,经两次降价后的每件售价![]() 元,每星期能卖出
元,每星期能卖出![]() 件.
件.
![]() 已知两次降价百分率相同,求每次降价的百分率;
已知两次降价百分率相同,求每次降价的百分率;
![]() 聪明的店主在降价过程中发现,适当的降价既可增加销售又可增加收入,且每件衬衫售价每降低
聪明的店主在降价过程中发现,适当的降价既可增加销售又可增加收入,且每件衬衫售价每降低![]() 元,销售会增加
元,销售会增加![]() 件,若店主想要每星期获利
件,若店主想要每星期获利![]() 元,应把售价定为多少元?
元,应把售价定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com