
【题目】如图,把菱形![]() 沿
沿![]() 折叠,
折叠,![]() 落在
落在![]() 边上的
边上的![]() 处,若
处,若![]() ,则
,则![]() 的大小为( )
的大小为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
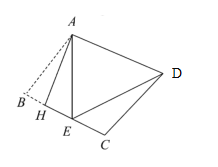
根据翻折变换的性质可得AB=AE,然后根据等腰三角形两底角相等求出∠B=∠AEB=70°,根据菱形的四条边都相等可得AB=AD,菱形的对角相等求出∠ADC,再求出∠DAE,然后根据等腰三角形两底角相等求出∠ADE,然后根据∠EDC=∠ADC-∠ADE计算即可得解.
解:∵菱形ABCD沿AH折叠,B落在BC边上的点E处,
∴AB=AE,
∵∠BAE=40°,
∴∠B=∠AEB=![]() (180°-40°)=70°,
(180°-40°)=70°,
在菱形ABCD中,AB=AD,∠ADC=∠B=70°,
AD∥BC,
∴∠DAE=∠AEB=70°,
∵AB=AE,AB=AD,
∴AE=AD,
∴∠ADE=![]() (180°-∠DAE)=
(180°-∠DAE)=![]() (180°-70°)=55°,
(180°-70°)=55°,
∴∠EDC=∠ADC-∠ADE=70°-55°=15°.
故选:B.


科目:初中数学 来源: 题型:
【题目】已知A、B在数轴上分别表示a,b.
(1)对照数轴填写下表:
a | 6 | -6 | -6 | -6 | 2 | -1.5 |
b | 4 | 0 | 4 | -4 | -10 | -1.5 |
A、B两点的距离 |
(2)若A、B两点间的距离记为d,试问:d和a,b有何数量关系?
(3)在数轴上标出所有符合条件的整数点P,使它到10和-10的距离之和为20,并求所有这些整数的和;
(4)找出(3)中满足到10和-10的距离之差大于1而小于5的整数的点P;
(5)若点C表示的数为x,当点C在什么位置时,![]() 取得的值最小?
取得的值最小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE.
(1)连接EC,如图①,试探索线段BC,CD,CE之间满足的等量关系,并证明你的结论;
(2)连接DE,如图②,求证:BD2+CD2=2AD2
(3)如图③,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°,若BD=![]() ,CD=1,则AD的长为 ▲ .(直接写出答案)
,CD=1,则AD的长为 ▲ .(直接写出答案)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k+1)x+4k﹣3=0.
(1)求证:无论k取什么实数值,该方程总有两个不相等的实数根;
(2)当Rt△ABC的斜边长a为![]() ,且两条直角边的长b和c恰好是这个方程的两个根时,求△ABC的周长.
,且两条直角边的长b和c恰好是这个方程的两个根时,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:
①abc>0;②b2=4ac; ③4a+2b+c>0;④3a+c>0,

其中,正确的结论是______.(写出正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产为正、减产为负):

(1)根据记录可知前三天共生产______辆;
(2)产量最多的一天比产量最少的一天多生产______辆;
(3)该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?请说明理由.
(4)若将上面第(3)问中“实行每周计件工资制”改为“实行每日计件工资制”,其他条件不变,在此方式下该厂工人这一周按日计件工资与按周计件的工资哪一个更多?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
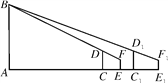
【题目】如图,学校的操场上有一旗杆AB,甲在操场上的C处竖立3 m高的竹竿CD;乙从C处退到E处恰好看到竹竿顶端D与旗杆顶端B重合,量得CE=3 m,乙的眼睛到地面的距离FE=1.5 m;丙在C1处竖立3 m高的竹竿C1D1,乙从E处后退6 m到E1处,恰好看到两根竹竿和旗杆重合,且竹竿顶端D1与旗杆顶端B也重合,量得C1E1=4 m.求旗杆AB的高.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com