
定义:如果一个 与
与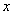 的函数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是
的函数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是 与
与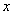 的“反比例平移函数”.
的“反比例平移函数”.
例如: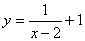 的图象向左平移2个单位,再向下平移1个单位得到
的图象向左平移2个单位,再向下平移1个单位得到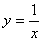 的图象,则
的图象,则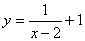 是
是 与
与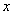 的“反比例平移函数”.
的“反比例平移函数”.
(1)若矩形的两边分别是2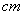 、3
、3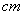 ,当这两边分别增加
,当这两边分别增加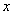 (
(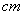 )、
)、 (
(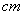 )后,得到的新矩形的面积为8
)后,得到的新矩形的面积为8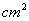 ,求
,求 与
与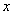 的函数表达式,并判断这个函数是否为“反比例平移函数”.
的函数表达式,并判断这个函数是否为“反比例平移函数”.
(2)如图,在平面直角坐标系中,点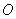 为原点,矩形
为原点,矩形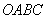 的顶点
的顶点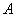 、
、 的坐标分别为(9,0)、(0,3) .点
的坐标分别为(9,0)、(0,3) .点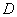 是
是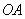 的中点,连接
的中点,连接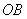 、
、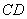 交于点
交于点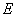 ,“反比例平移函数”
,“反比例平移函数”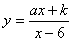 的图象经过
的图象经过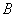 、
、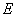 两点.则这个“反比例平移函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式 .
两点.则这个“反比例平移函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式 .
( 3)在(2)的条件下, 已知过线段
3)在(2)的条件下, 已知过线段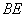 中点的一条直线
中点的一条直线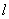 交这个“反
交这个“反
比例平移函数”图象于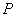 、
、 两点(
两点(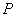 在
在 的右侧),若
的右侧),若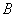 、
、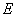 、
、
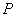 、
、 为顶点组成的四边形面积为16,请求出点
为顶点组成的四边形面积为16,请求出点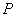 的坐标.
的坐标.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
□ABCD的对角线相交于点O,分别添加下列条件:①AC⊥BD;②AB=BC;③AC平分∠BAD;④AO=DO,使得□ABCD是菱形的条件有 。(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
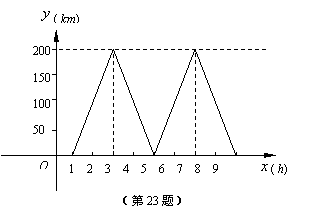
某物流公司的快递车和货车每天往返于甲、乙两地,快递车比货车多往返一趟.
已知货车比快递车早1小时出发,到达乙地后用1小时装卸货物,然后按原路以原速返回,
结果与第二趟返回的快递车同时到达甲地.下图表示快递车距离甲地的路程y(km)与货
车出发所用时间x(h)之间的函数关系图象.
(1)①请在下图中画出货车距离甲地的路程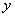 (km)与所用时间
(km)与所用时间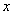 ( h)的函数关系图象;
( h)的函数关系图象;
②两车在中途相遇 次.
(2)试求货车从乙地返回甲地时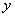 (km)与所用时间
(km)与所用时间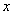 ( h)的函数关系式.
( h)的函数关系式.
(3)求快递车第二次从甲地出发到与返程货车相遇所用时间为多少h?这时货车离
乙地多少km?
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
2014年春季,北京持续多天的雾霾天气让环保和健康问题成为人们关注的焦点.为了美丽的北京和师生的身心健康,某校开展以“倡导绿色出行,关爱师生健康”为主题的教育活动.为了了解本校师生的出行方式,在本校范围内随机抽查了部分师生,将收集的数据绘制成下列不完整的两种统计图.
|

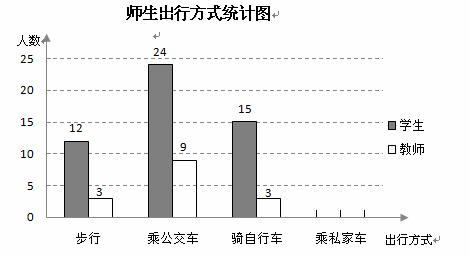
请根据统计图提供的信息,解答下列问题:
(1)m = ;
(2)已知随机抽查的教师人数为学生人数的一半,请根据上述信息补全条形统计图,并标明相应数据;
(3)若全校师生共1800人,请你通过计算估计,全校师生乘私家车出行的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系 中,点
中,点 ,
,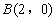 ,正六
,正六 边形
边形 沿
沿 轴正方向无滑动滚动,当点
轴正方向无滑动滚动,当点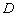 第一次落在
第一次落在 轴上时,点
轴上时,点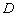 的坐标为: ;在运动过程中,点
的坐标为: ;在运动过程中,点 的纵坐标的最大值是 ;保持上述运动过程,经过
的纵坐标的最大值是 ;保持上述运动过程,经过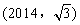 的正六边形的顶点是 。
的正六边形的顶点是 。
 | |||
 | |||
查看答案和解析>>
科目:初中数学 来源: 题型:
如图, Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E为BC边的中点,连接DE.
 (1)求证:DE与⊙O 相切.
(1)求证:DE与⊙O 相切.
(2)若tanC= ,DE=2,求AD的长.
,DE=2,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com